1. 计算机组成原理概述
计算机:数字电子计算机
组成:计算机硬件系统的逻辑实现
原理:不以具体机型为依托的,基本实现原理。
计算机组成原理:掌握如何实现的具体细节。
1.1 计算机系统简介
计算机系统由两大部分组成:硬件和软件。
- 硬件:
- 计算机的实体,如主机、外设等。
- 软件:
- 由具有各类特殊功能的程序组成
软件又包括系统软件和应用软件。
系统软件可以管理整个计算机系统:
- 语言处理程序(将高级语言转换为机器可以懂的指令)
- 操作系统
- 服务性程序(比如数学库、MPI服务程序进行并行之间的通信)
- 数据库管理系统
- 网络软件
应用软件是按照任务需要编制成的程序。
可以简单将软硬件看作一个层次结构,硬件为软件提供接口,系统软件又为应用软件形成接口,来完成不同的程序。
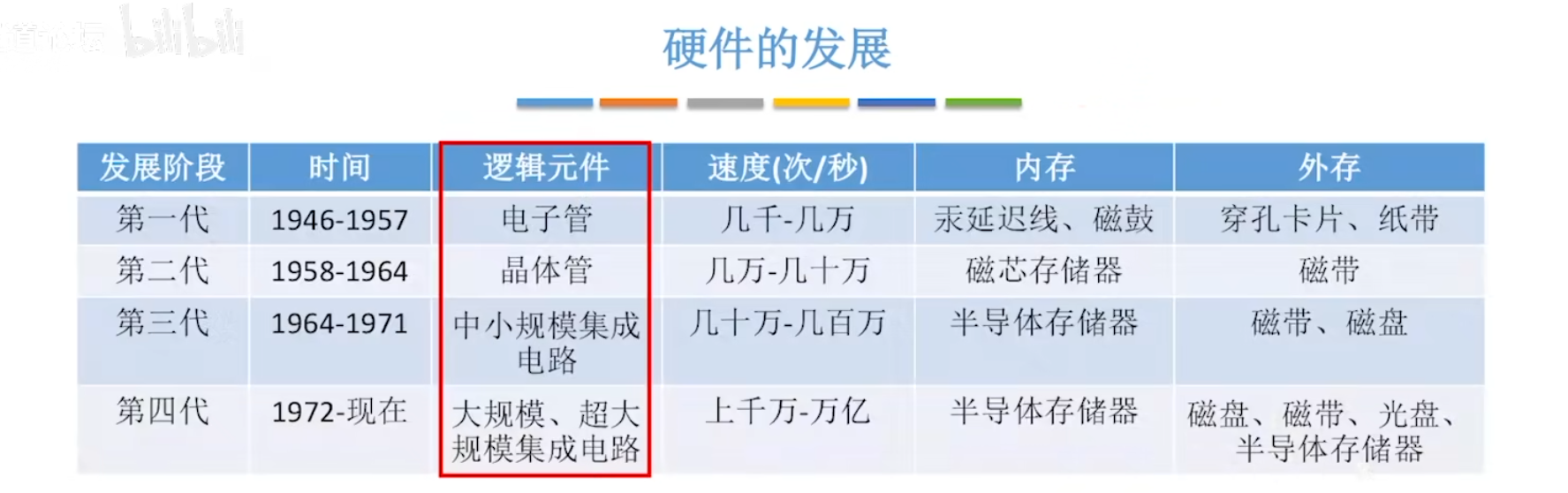
硬件的发展:
- 第一代:电子管时代
- 第二代:晶体管时代
- 第三代:中小规模集成电路时代
- 第四代:大规模、超大规模集成电路时代
微处理器的发展:
微型计算机的发展以为处理器技术为标准
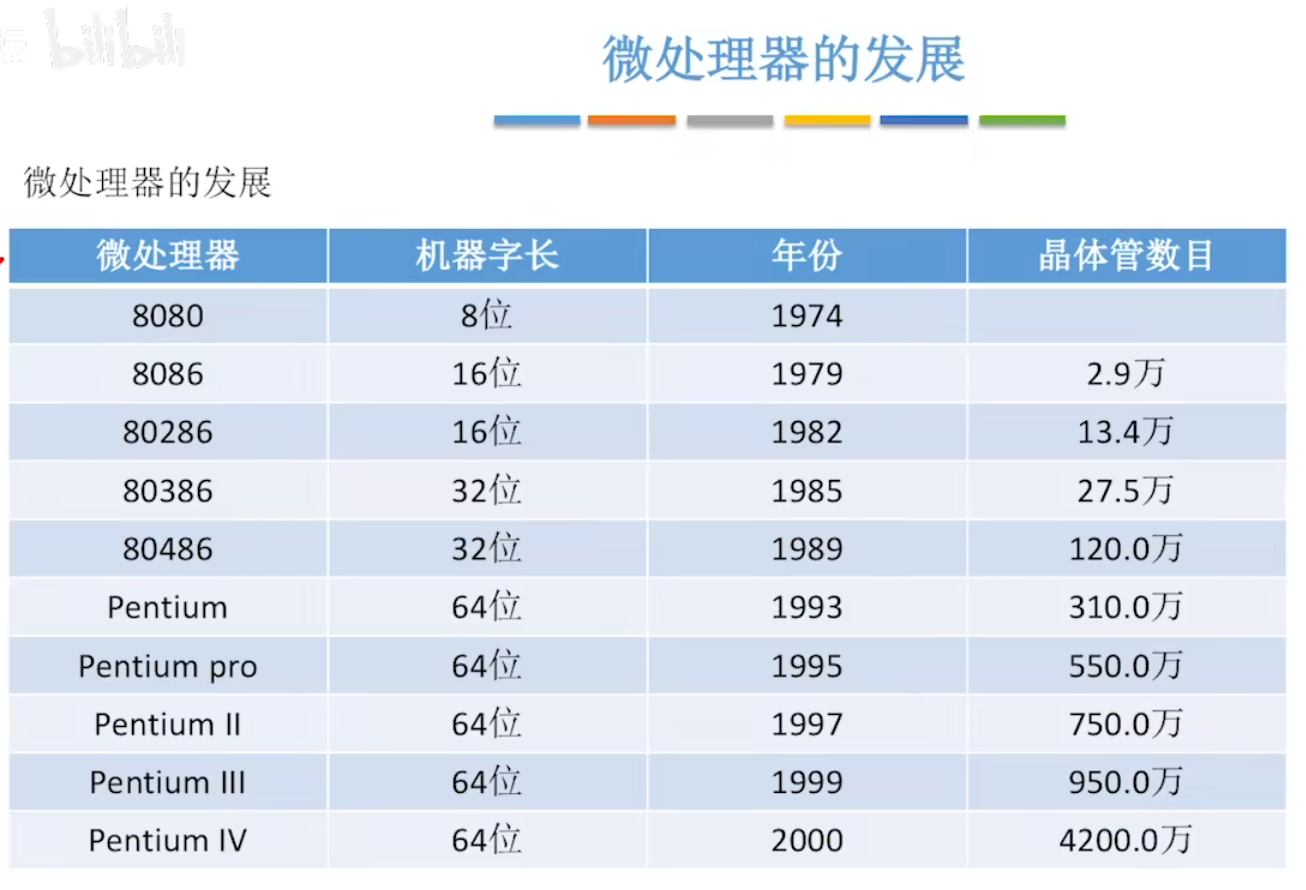
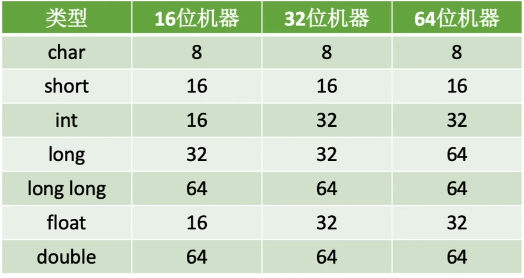
机器字长:计算机一次整数运算所能处理的二进制位数。
硬件的发展
- 1947年,贝尔实验室,发明了“晶体管”
- 1955年,肖克利在硅谷创建肖克利实验室股份有限公司1957年,八叛徒(traitorous eight)创立仙童半导体公司1959年,仙童半导体公司发明“集成电路”
- 1968年,摩尔等人离开仙童,创立Intel
- 1969年,仙童销售部负责人桑德斯离开仙童,创立AMD
摩尔定律:
揭示了信息技术进步的速度
集成电路上可容纳的晶体管数目,约每隔18个月便会增加一倍,整体性能也将提升一倍
软件的发展
目前的发展趋势:“两极”分化
- 一极是微信计算机向更微型化、网络化、高性能、多用途的方向发展
- 另一极向更巨型化、超高速、并行处理、智能化方向发展
1.2计算机硬件的基本组成
1.2.1冯诺依曼机和现代计算机
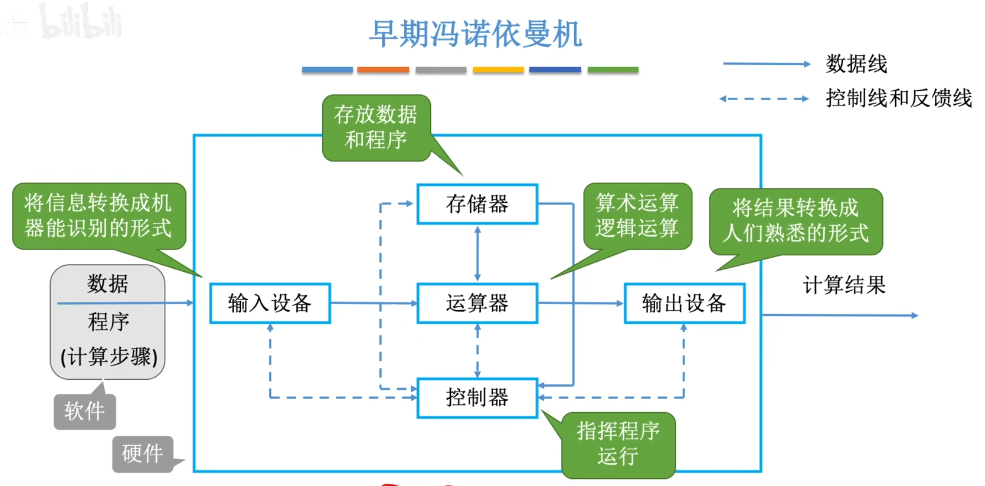
冯诺依曼机
“存储程序”的概念是指将指令以二进制代码的形式事先输入计算机的主存储器,然后按其在存储器中的首地址执行程序的第一条指令,以后就按该程序的规定顺序执行其他指令,直至程序执行结束。
在计算机系统中,软件和硬件在逻辑上是等效的。
Eg:对于乘法运算,可以设计一个专门的硬件电路实现乘法运也可以用软件的方式,执行多次加法运算来实现
冯诺依曼机的特点:
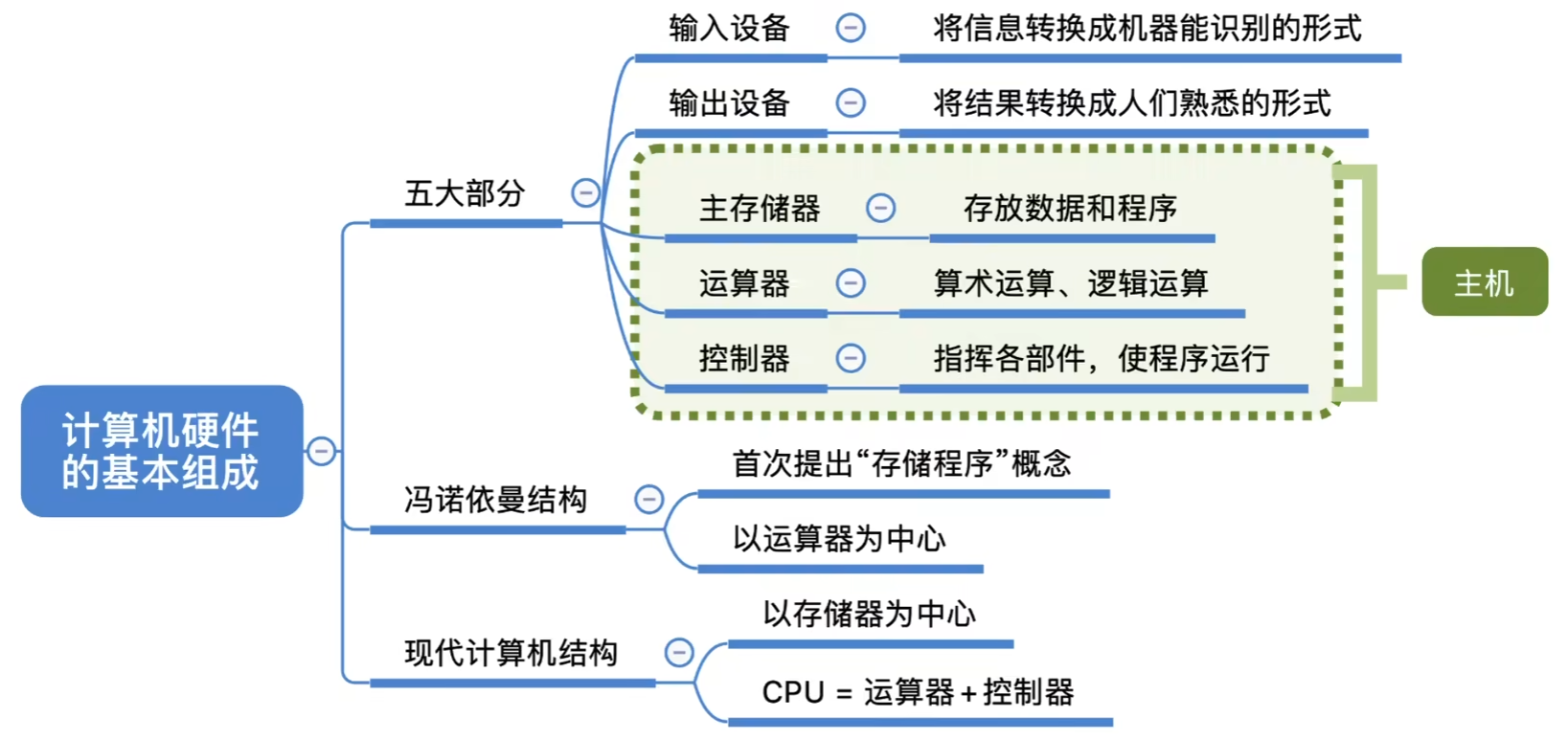
计算机由五大部件组成
- 输入设备
- 存储器
- 运算器
- 控制器
- 输出设备
输入设备和输出设备统称为I/O设备
指令和数据以同等地位存于存信器,可按地址寻访
- 指令和数据用二进制表示
- 指令由操作码和地址码组成
- 操作码:指明是什么操作(加减乘除)
- 地址码:要操作数据的地址
- 存储程序
- 提前把指令和数据存储到存储器当中
- 以运算器为中心
- 输入/输出设备与存储器之间的数据传送通过运算器完成
简单化理解就是:
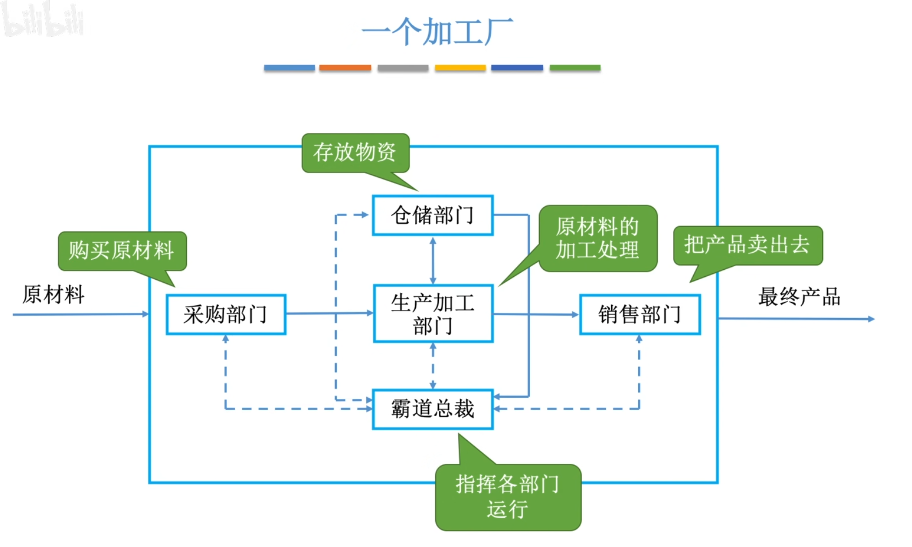
现代计算机的结构:
以存储器为中心
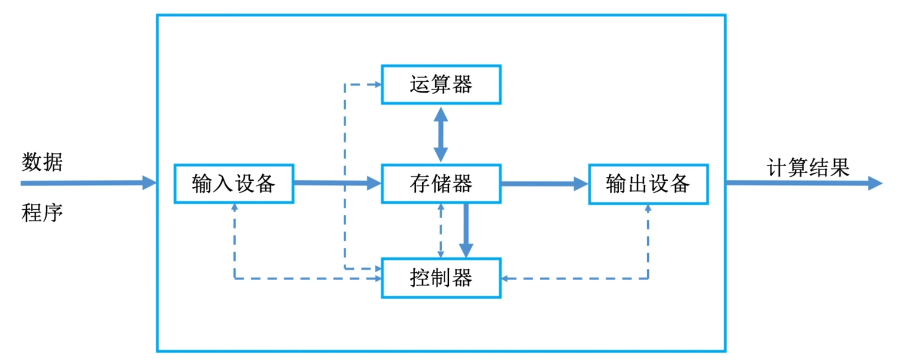
CPU = 运算器 + 控制器
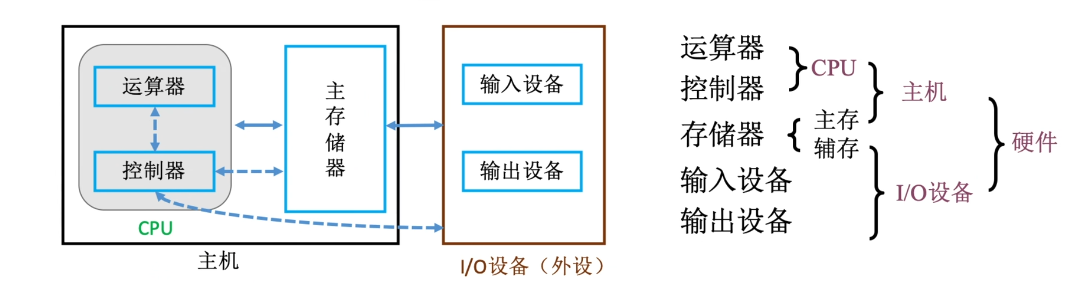
总结:
1.2.2硬件部件:
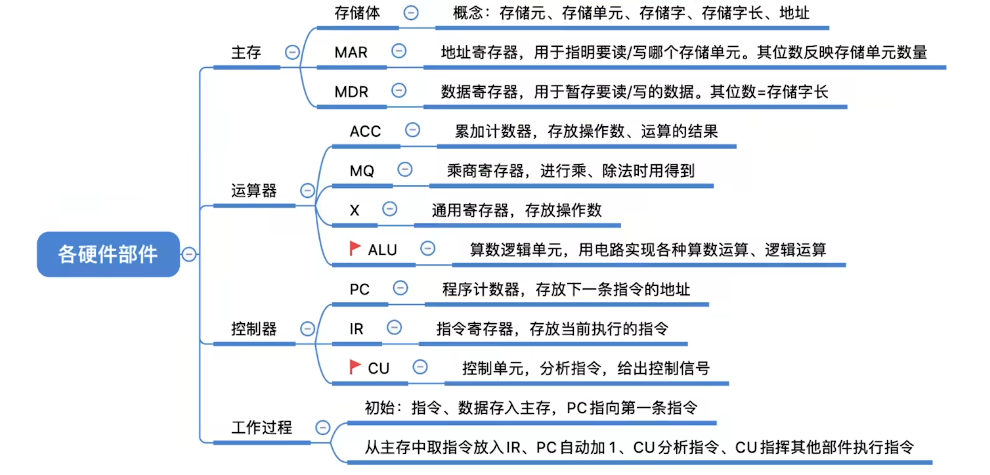
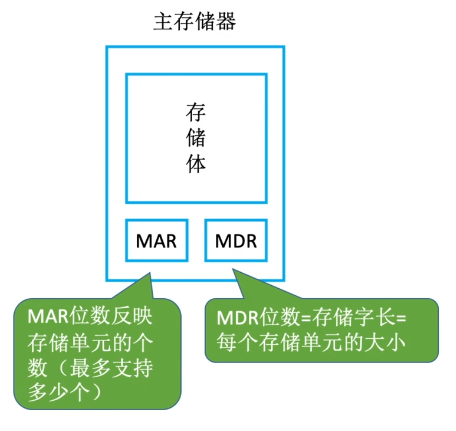
主存储器的基本组成
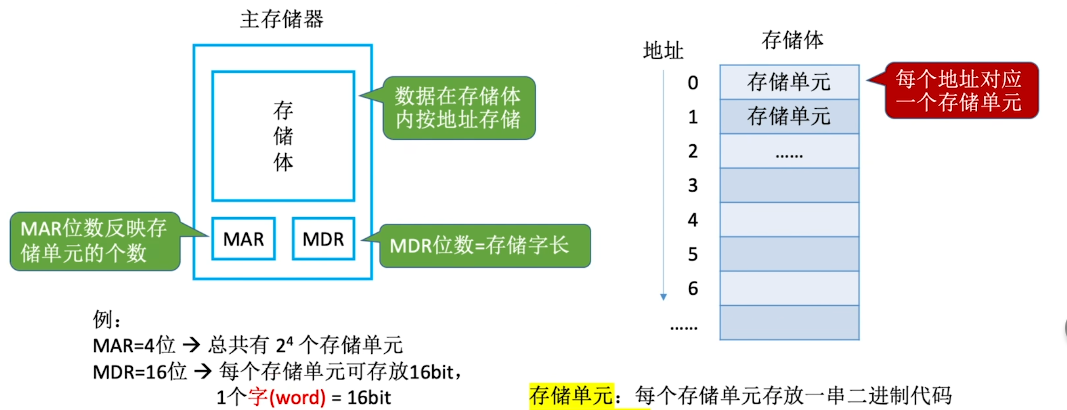
- Memory Address Register(存储地址寄存器)
- Memory Data Register(存储数据寄存)
- 存储单元:每个存储单元存放一串二进制代码
- 存储字(word):存储单元中二进制代码的组合
- 存储字长:存储单元中二进制代码的位数
- 存储元:即存储二进制的电子元件,每个存储元课存储1bit
易混淆:
- 一个字节(Byte) = 8bit
- 1B = 1个字节,1b=1个bit
运算器的基本组成:
运算器:用来实现算术运算(如:加减乘除、逻辑运算【与或非】)

- ACC:累加器,用于存放操作数,或运算结果。
- MQ:乘商寄存器,在乘、除运算时,用于存放操作数或运算结果。
- x:通用的操作数寄存器,用于存放操作数
- ALU:算术逻辑单元,通过内部复杂的电路实现算数运算、逻辑运算
控制器的基本组成:

- cu:控制单元,分析指令,给出控制信号
- IR:指令寄存器,存放当前执行的指令
- PC::序计数器,存放下一条指令地址,有自动加1功能
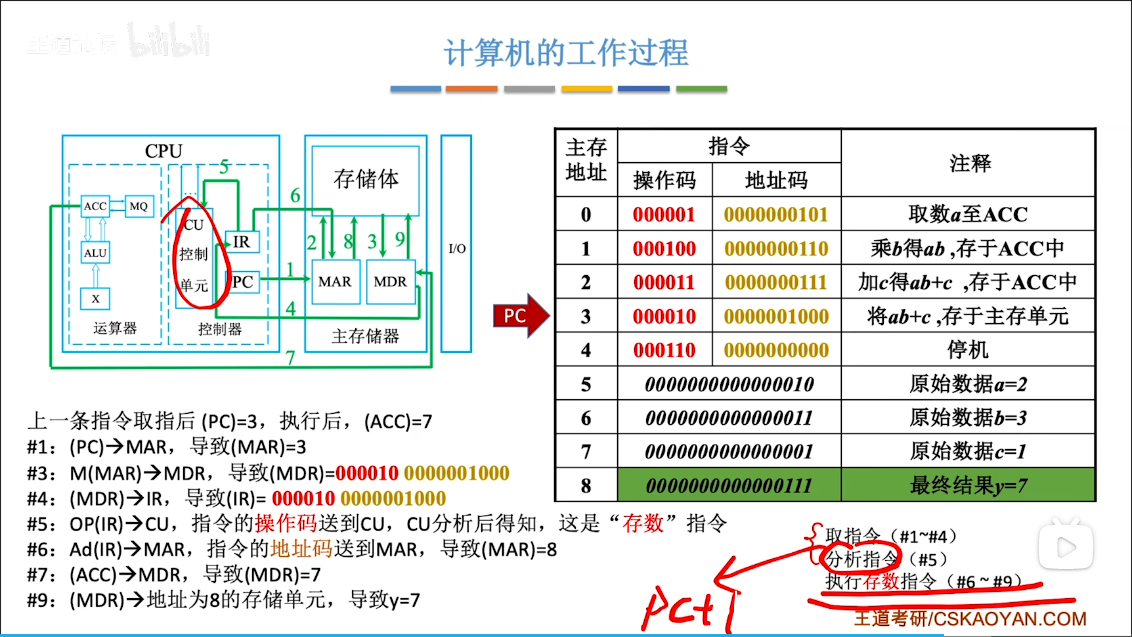
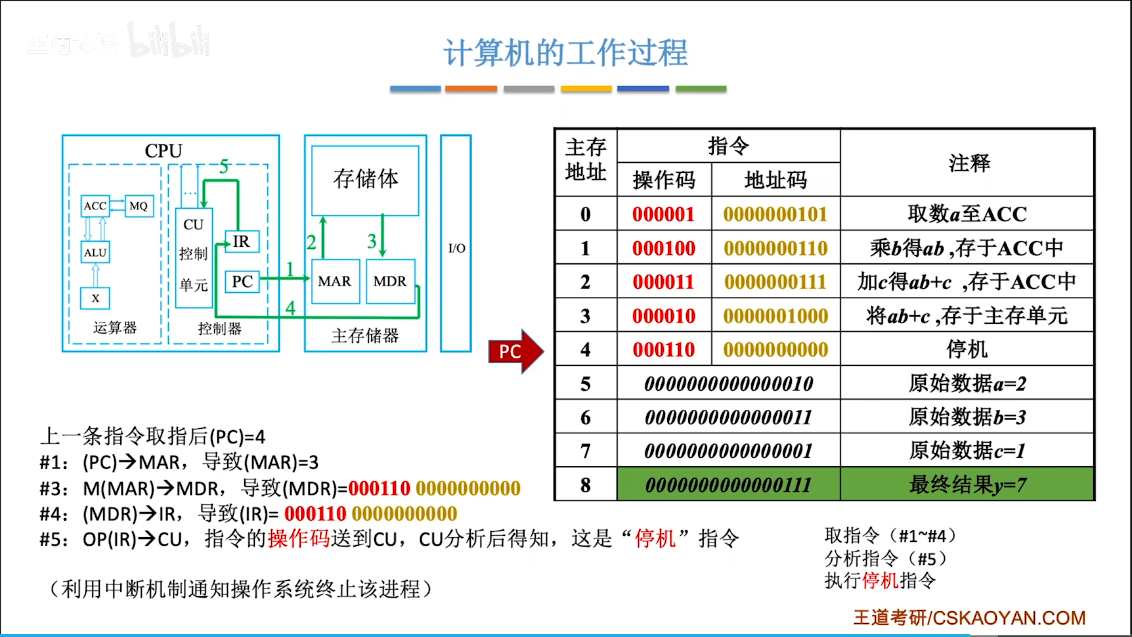
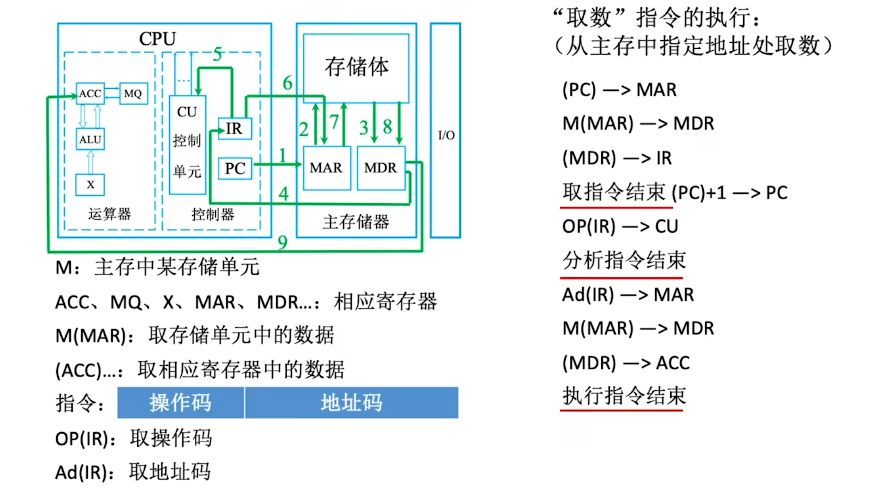
完成一条指令:

计算机的工作过程:
高级语言
int a=2,b=3,c=1,y=0;
void main(){
y=a*b+c;
}编译装入主存:
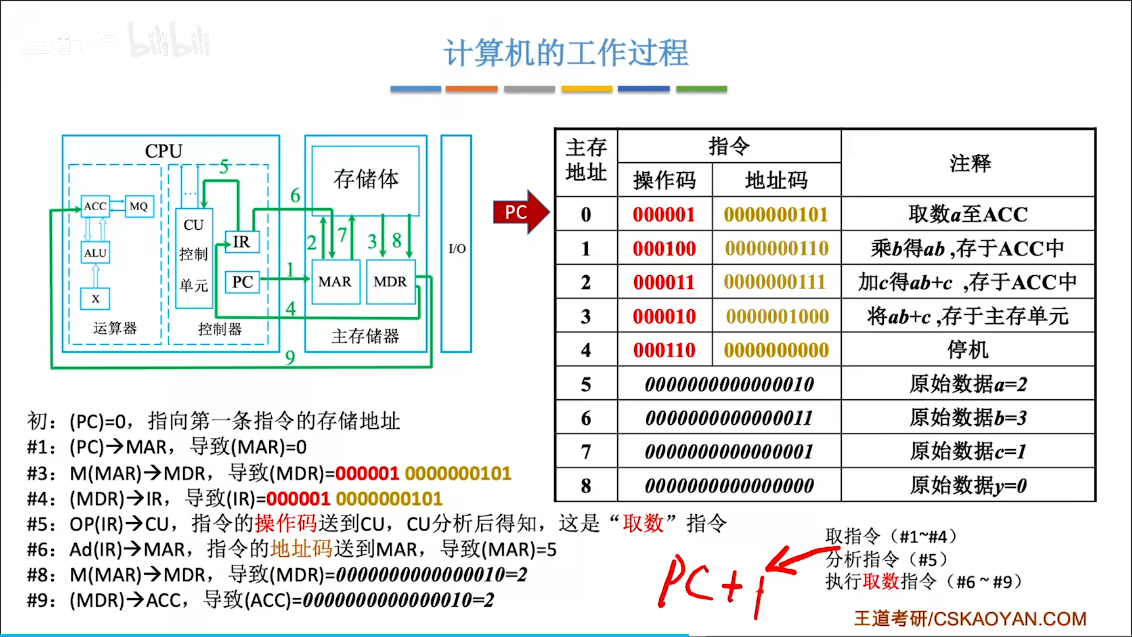
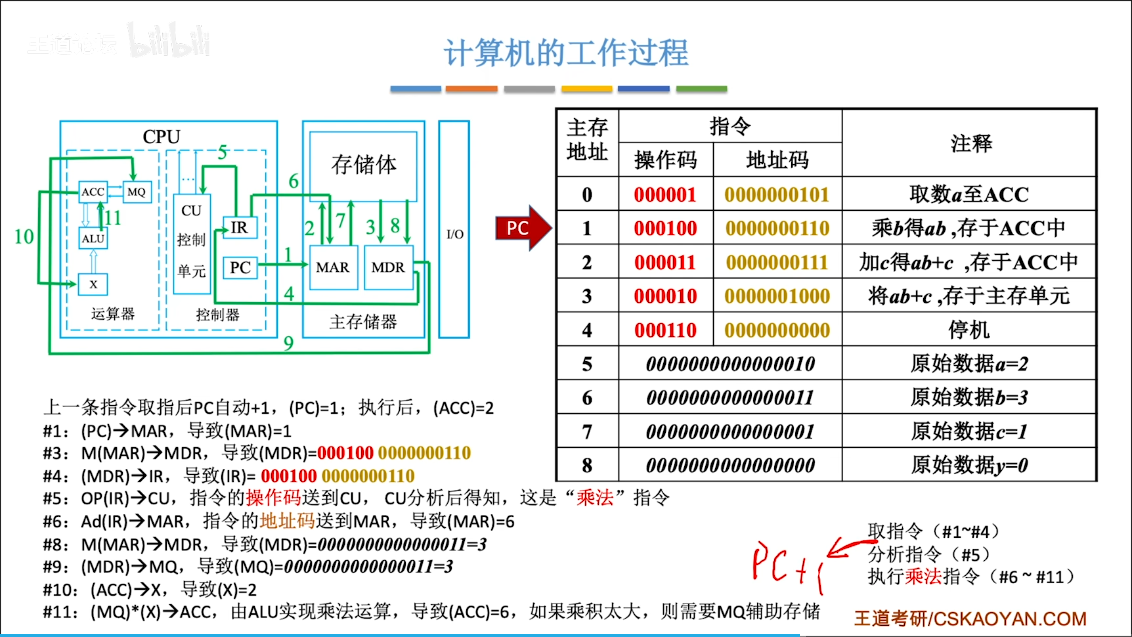
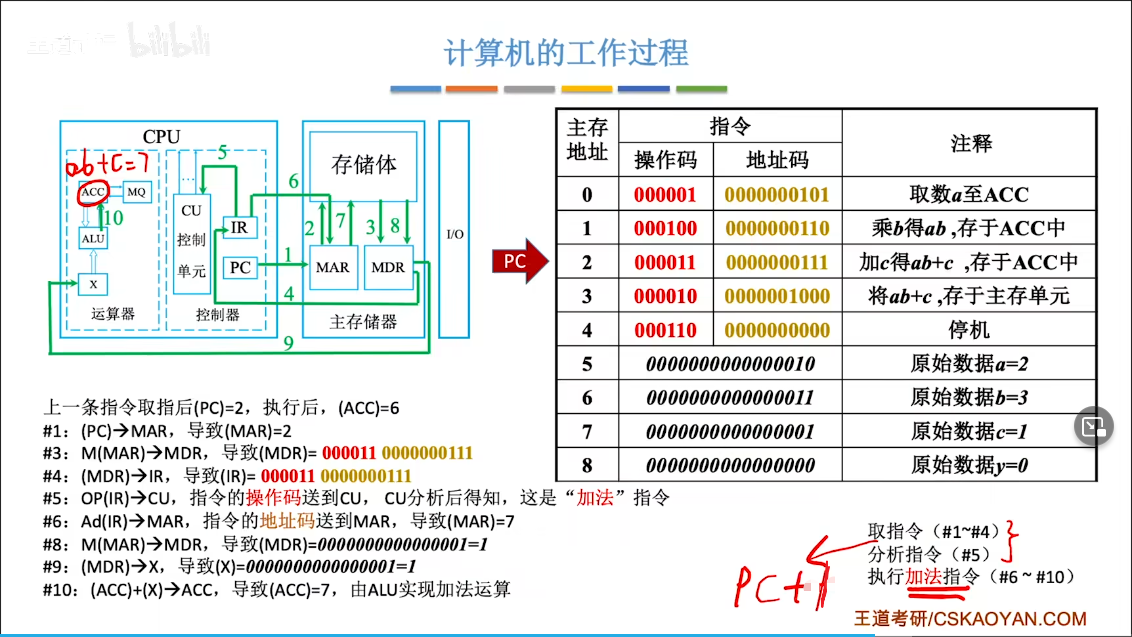
回顾:
重点;
注:现在的计算机通常把MAR、MDR集成在CPU中
1.2.3计算机系统的层次结构
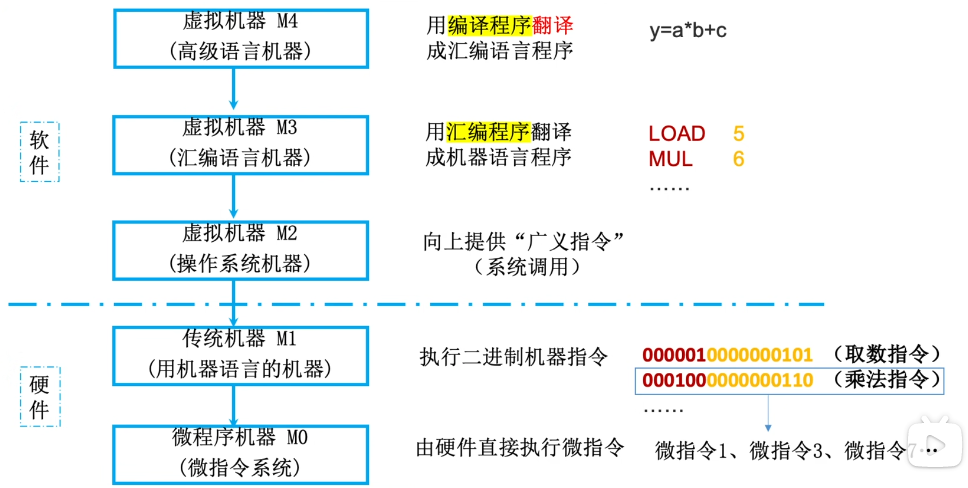
下层是上层的基础,上层是下层的拓展
三种级别的语言:
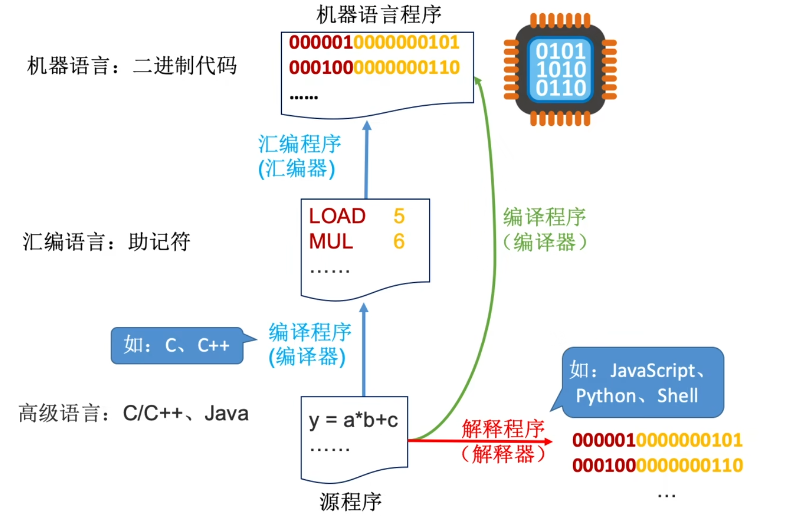
- 编译程序:将高级语言编写的源程序全部语句一次全部翻译成机器语言程序,而后再执行机器语言程序(只需翻译一次)
- 解释程序:将源程序的一条语句翻译成对应于机器语言的语句,并立即执行。紧接着再翻译下一句(每次执行都要翻译)
回顾:
计算机体系结构VS计算机组成原理
- 计算机体系结构:机器语言程序员所见到的计算机系统的属性概念性的结构与功能特性(指令系统、数据类型、寻址技术、I/o机理)
- 如何设计硬件与软件之间的接口
- 计算机组成原理:实现计算机体系结构所体现的属性,对程序员“透明”(具体指令的实现)
- 如何用硬件实现所定义的接口
1.3计算机的性能指标
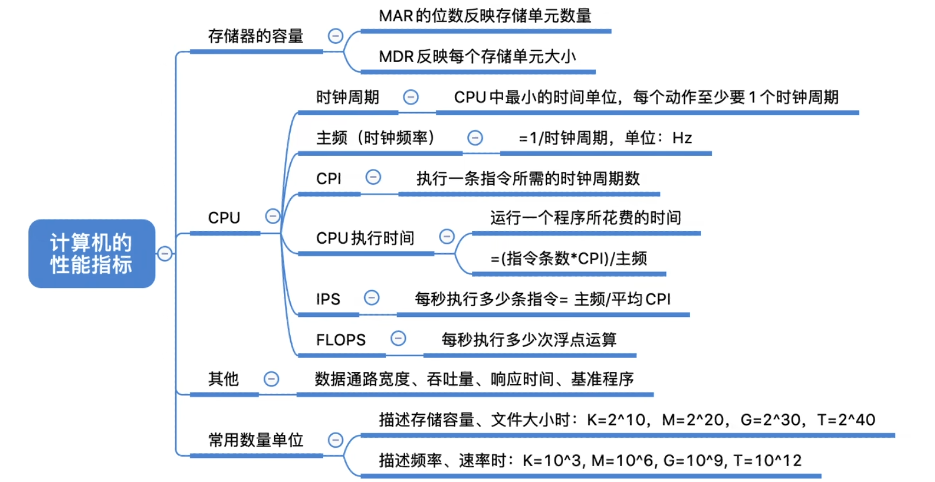
存储器的性能指标
1 Byte = 8 bit
总容量 = 存储单元个数 * 存储字长 bit
= 存储单元个数 * 存储字长 /8 Byte
Eg:MAR 为32 位,MDR为8位,总容量 = 2^32 * 8 bit = 4GB
n 个二进制位能表示出多少种不同的状态?

2^10:K 2^20:M 2^30:G 2^40 :T
CPU的性能指标
CPU主频: CPU内数字脉冲信号振荡的频率
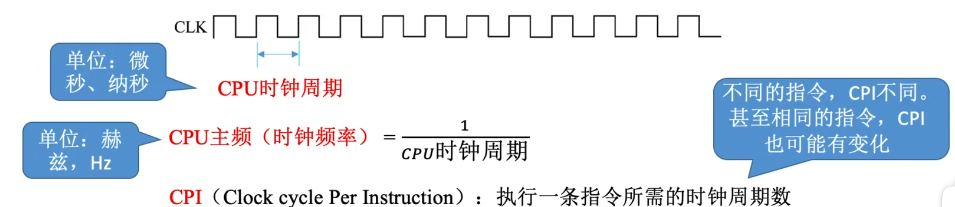
执行一条指令的耗时 = CPI * CPU时钟周期
Eg:某CPU主频为1000Hz,某程序包含100条指令,平均来看指令的CPl=3。该程序在该CPU上执行需要多久?
100 3 1/1000 = 0.3S
CPU执行时间(整个程序的耗时) = CPU时钟周期数/主频 = (指令条数 * CPI) / 主频
IPS(Instructions Per Second):每秒执行多少条指令
- IPS = 主频 / 评价CPI
FLQPS (Floating-point Operations Per Second) :每秒执行多少次浮点运算

系统整体的性能指标
数据通路带宽:数据总线一次所能并行传送信息的位数(各硬件部件通过数据总线传输数据)
吞吐量:指系统在单位时间内处理请求的数量。
- 它取决于信息能多快地输入内存,CPU能多快地取指令,数据能多快地从内存取出或存入,以及所得结果能多快地从内存送给一台外部设备。这些步骤中的每一步都关系到主存,因此,系统吞吐量主要取决于主存的存取周期。
响应时间:指从用户向计算机发送一个请求,到系统对该请求做出响应并获得它所需要的结果的等待时间。
- 通常包括CPU时间(运行一个程序所花费的时间)与等待时间(用于磁盘访问、存储器访问、I/o操作、操作系统开销等时间)。
基准程序:是用来测量计算机处理速度的一种实用程序,以便于被测量的计算机性能可以与运行相同梅予的其它计算机性能进行比较。’
几个问题:
- 主频高的CPU一定比主频低的CPu快吗?
- 不一定,如两个CPU,A的主频为2GHz,平均CPI=10;B的主频1GHz,平均CPl=1…
- 若A、B两个cPU的平均CPI相同,那么A一定更快吗?
- 也不一定,还要看指令系统,如A不支持乘法指令,只能用多次加法实现乘法;而B支持乘法指令。
- 基准程序执行得越快说明机器性能越好吗?
- 基准程序中的语句存在频度差异,运行结果也不能完全说明问题
总结:
2、数据的表示和运算
2.1 数制与编码
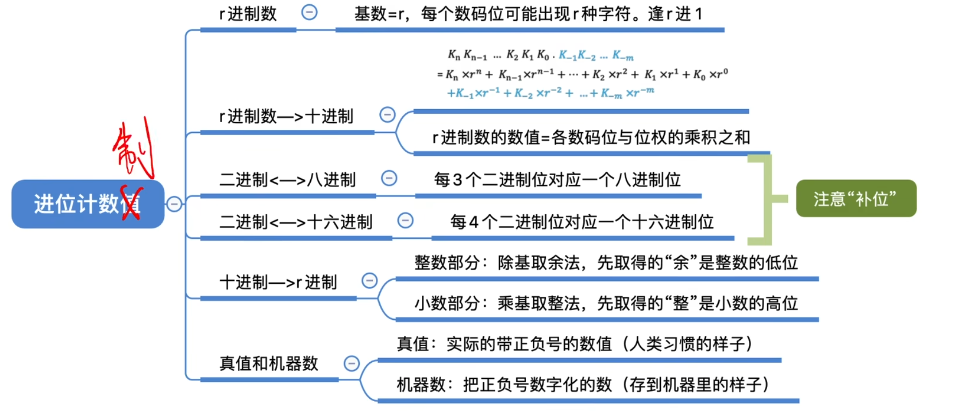
2.1.1进位计数制
r进制计数法

任意进制—-> 十进制

二进制 <—>八进制、十六进制
如:1111000010.01101
- 二进制 -> 八进制

- 二进制 -> 十六进制

- 八进制 - > 二进制

- 十六进制 -> 二进制

各种进制的常见书写方式
- 二进制
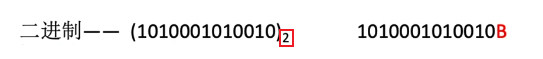
- 八进制
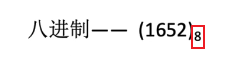
- 十六进制

- 十进制

十进制 -> 任意进制
取整/余法
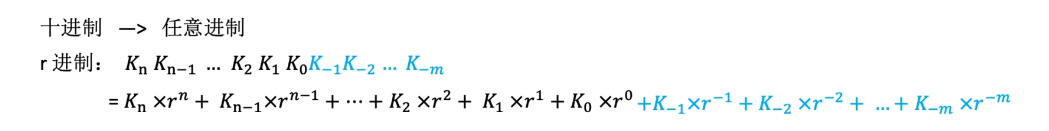
如:75.3 整数部分75
除基取余法

小数部分:0.3
乘基取整法

拼凑法
比如十进制数:260.75 、 533.125

直接比较拼凑
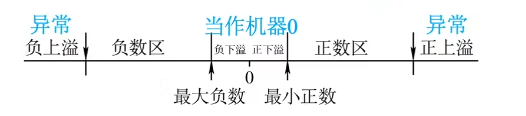
真值和机器数
- 真值
- 符合人类习惯的数字
- 机器数
- 数字实际存到机器里的形式,正负号需要被“数字化”
回顾
注意:有的十进制小数无法用二进制精确表示,如:0.3
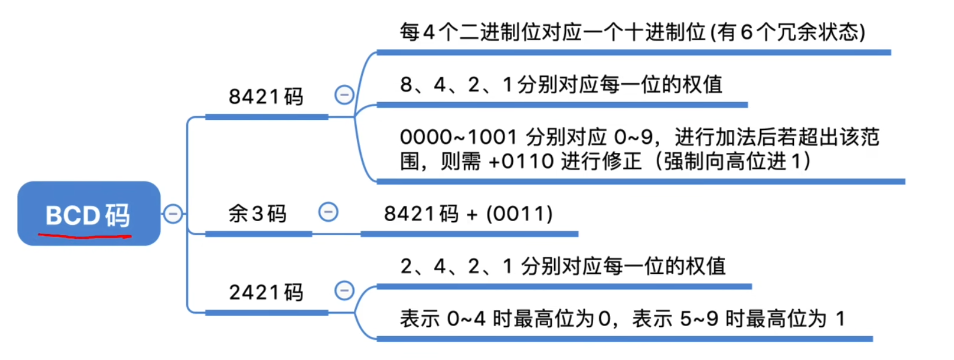
2.1.2 BCD码
8421码
8421码的映射关系:
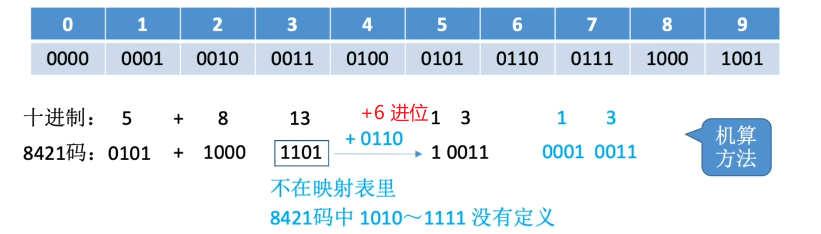
4个二进制位 -> 16种不同的状态
BCD码只使用其中10种 - > 不同的映射方案
注:若相加结果在合法范围内,则无需修正。
余3码:

2421码
改变权值定义 四位的权重分别是 2 4 2 1

规定:在5之后,第一位只能是1
总结
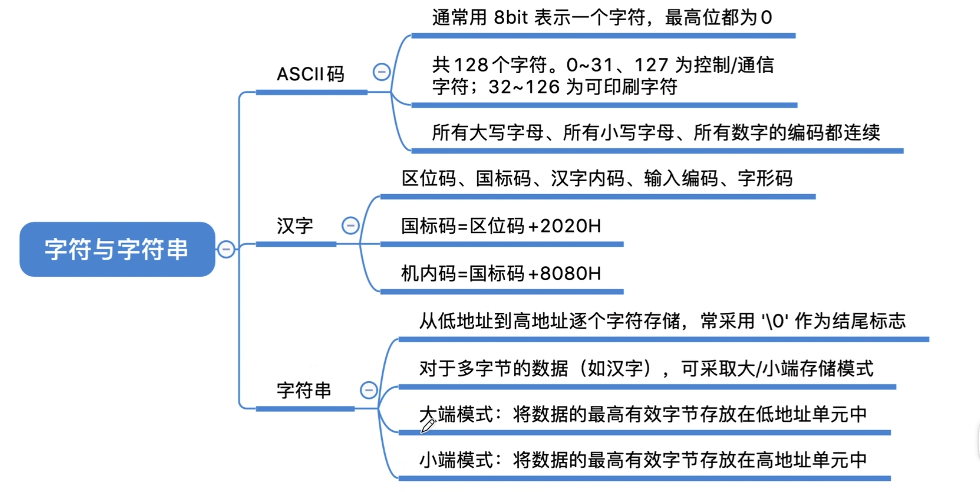
2.1.3字符与字符串
ASCII码
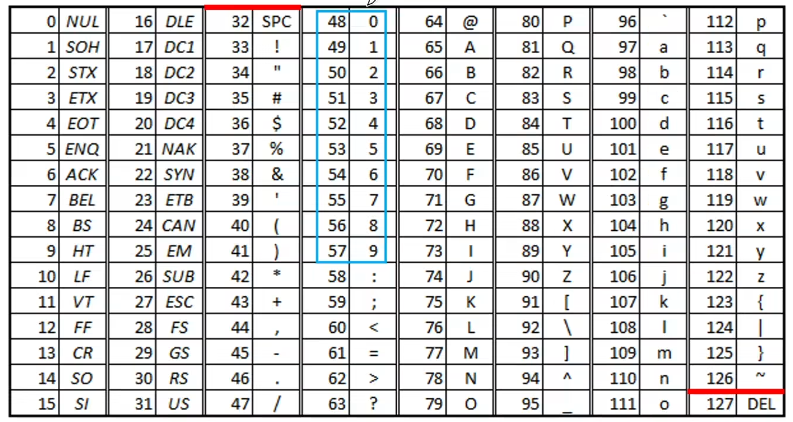
- 可印刷字符:32~126,其余为控制、通信字符
- 数字:48(0011 0000)~ 57(0011 1001)
- 前四位(4个bit位)相同,后面的符合8421码编码
- 大写字母:65(0100 0001)~ 90 (0101 1010)
- 前三位(3个bit位)相同,后面的是1~26
- 小写字母:97(0110 0001)~ 122(0111 1010)
- 前三位(3个bit位)相同,后面的是1~26
汉字的表示和编码
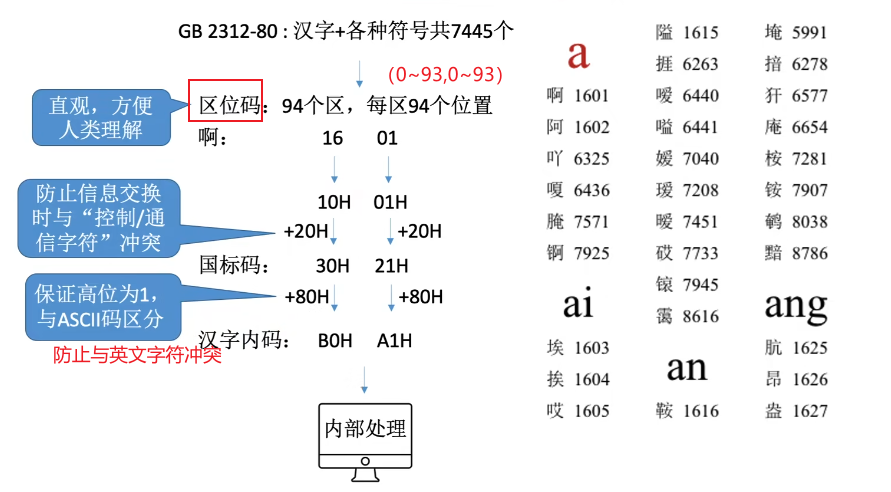
输入:输入编码
- 如拼音、五笔输入法
输出:汉字字形码
字符串
不带中文字符的:
某计算机按字节编址(每个地址对应1B),从地址为2的单元开始,存储字符串”abc”。

各字符的ASCII编码
- a:0110 0001 = 61H
- b:0110 0010 = 62H
- c:0100 0011 = 63H
- \0: 0000 0000 = 00H
- 很多语言中,’\0’作为字符串结尾的标志
带有中文字符的
某计算机按字节编址(每个地址对应1B),从地址为2的单元开始,存储字符串”abc啊”。
各字符的ASCII编码
- a:0110 0001 = 61H
- b:0110 0010 = 62H
- c:0100 0011 = 63H
- 啊: 机内码 = B0 A1H
- \0: 0000 0000 = 00H
- 很多语言中,’\0’作为字符串结尾的标志
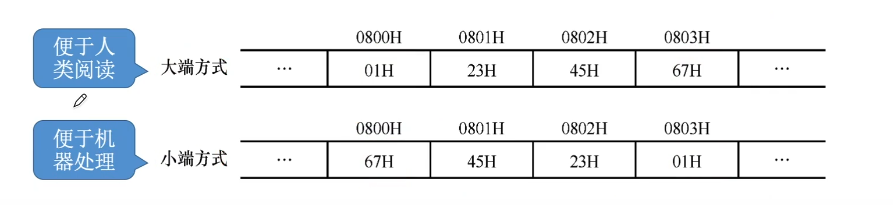
在所有计算机中,多字节数据都被存放在连续的字节序列中。根据数据中各字节的排列顺序不同,可能有“大端模式”、“小端模式”
大端模式
将数组的最高有效字节存放到低地址单元中

小端模式
将数组的最高有效字节存放到高地址单元中

总结
2.1.4奇偶校验码
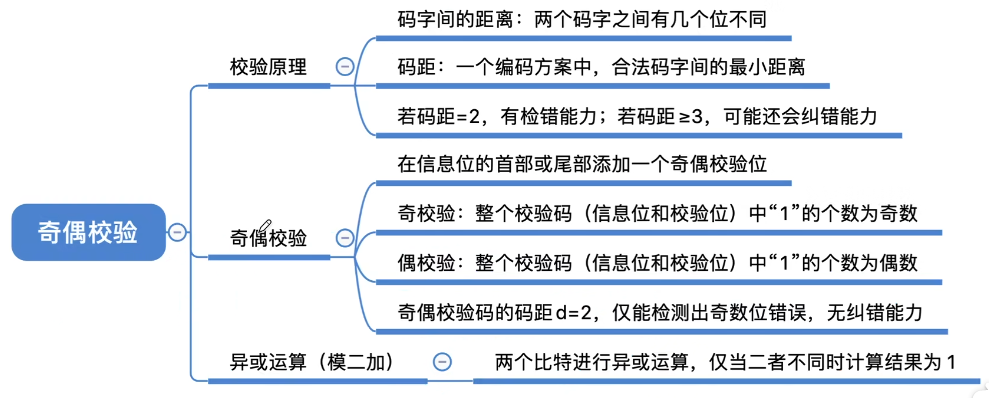
校验原理简介
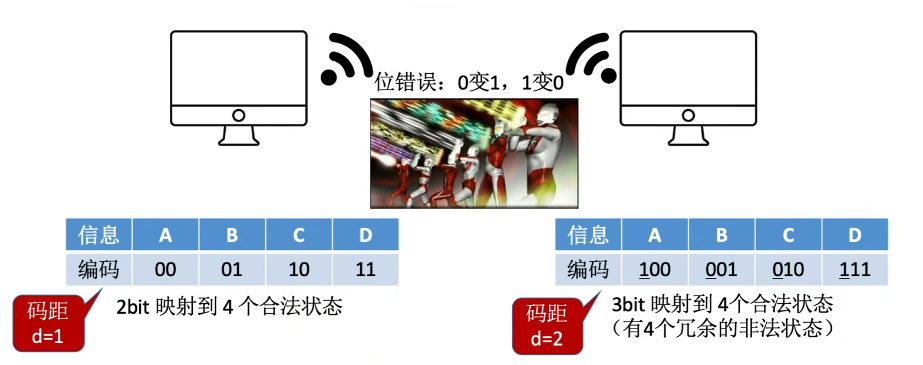
- 由若干位代码组成的一个字叫码字。
- 将两个码字逐位进行对比,具有不同的位的个数称为两个码字间的距离.
- 一种编码方案可能有若干个合法码字,各合法码字间的最小距离称为“码距”。
当d=1时,无检错能力;当d=2时,有检错能力;当d>=3时,若设计合理,可能具有检错、纠错的能力。
奇校验码:整个校验码(有效信息位和校验位)中“1”的个数为奇数。
偶校验码:整个校验码(有效信息位和校验位)中“1”的个数为偶数。
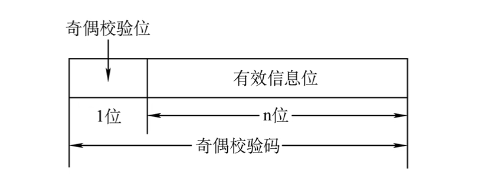
【例】给出两个编码1001101和1010111的奇校验码和偶校验码。设最高位为校验位,余7位是信息位,则对应的奇偶校验码为:
奇校验:1001101(11001101) 1010111(01010111)
偶校验:1001101(01001101) 1010111(11010111)
偶校验的硬件实现:
各信息进行异或(模2加)运算,得到的结果为1说明出错。

总结
2.1.5海明校验码
设计思路:将信息位分组进行偶校验 -> 多个校验位 -> 多个校验位标注出错位置
需要多少校验位?
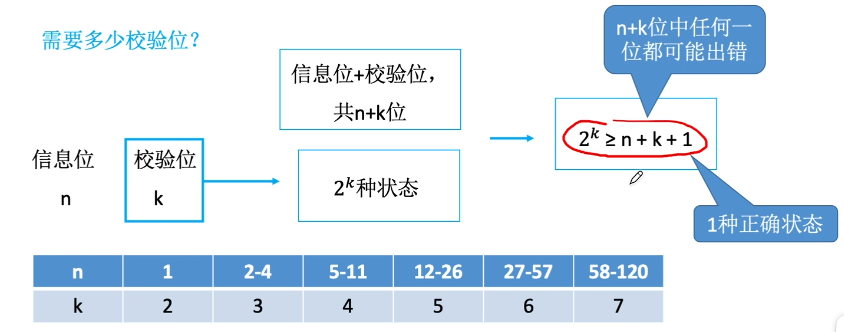
海明码求解步骤:
信息位:1010
1、确定海明码的位数:2^k >= n+k+1

2、确定校验位的分布
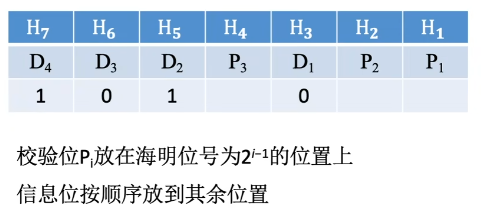
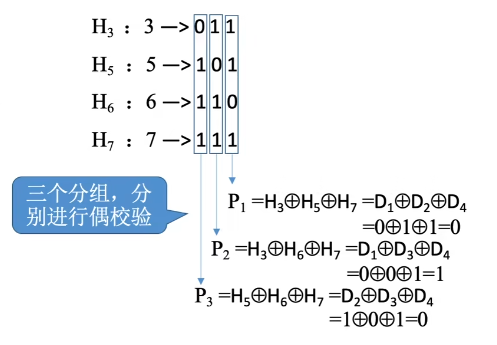
3、求校验位的值
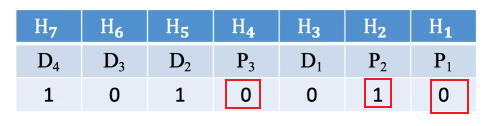
4、纠错
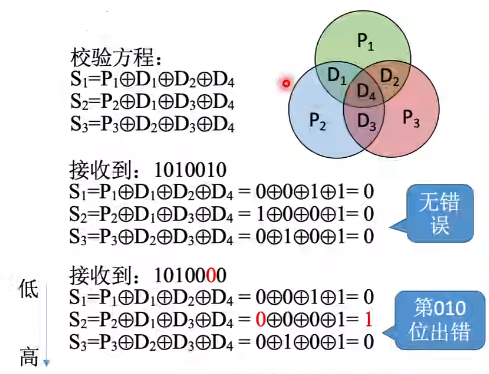
海明码的检错、纠错能力:
- 纠错能力— 1位
- 检错能力— 2位
总结
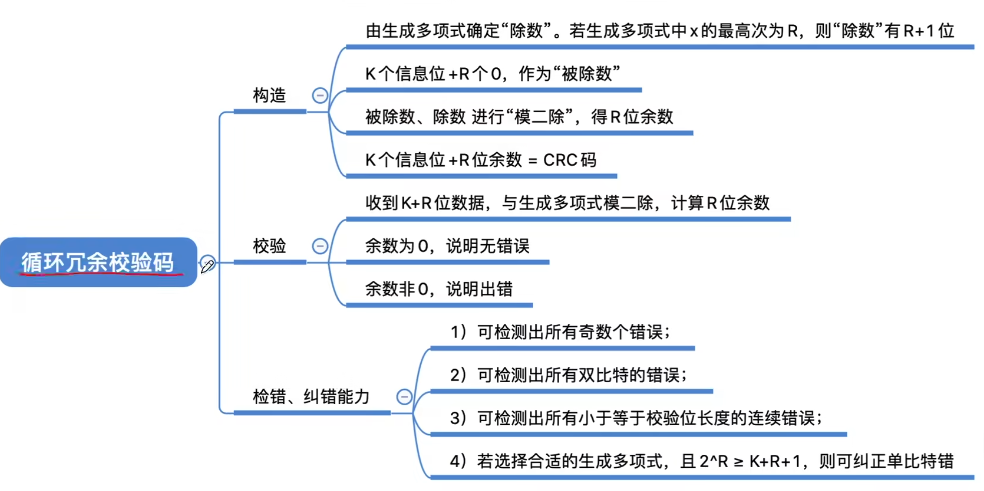
2.1.6 循环冗余校验码
循环冗余校验(Cyclic Redundancy Check,CRC)
循环冗余校验码的思想:
- 数据发送、接受方约定一个“除数”
- k个信息位+R个校验位作为“被除数”,添加校验位后需保证除法的余数为0
- 收到数据后,进行除法检查余数是否为0
- 若余数非0说明出错,则进行重传或纠错
实现方式
【例】设生成多项式为
- 1.确定K、R以及生成多项式对应的二进制码
K=信息码的长度=6,R=生成多项式最高次幂=3→ 校验码位数 N=K+R=9
生成多项式
- ⒉移位
信息码左移R位,低位补0
- 3.相除
对移位后的信息码,用生成多项式进行模2除法,产生余数

对应的CRC码:101001 001
- 4.检错和纠错
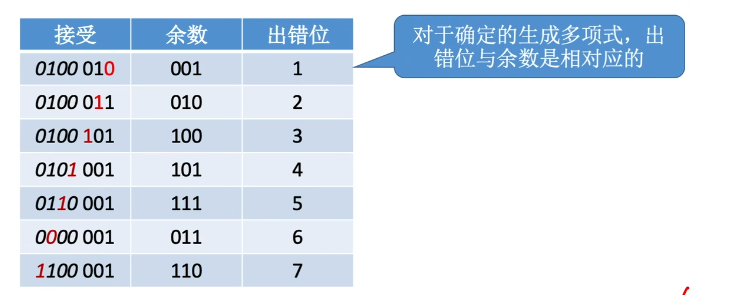
发送:101001001 记为
接收:101001001 用1101 进行模2除$-> 余数为000,代表没有出错
接收:101001011 用1101 进行模2除 -> 余数为010,代表
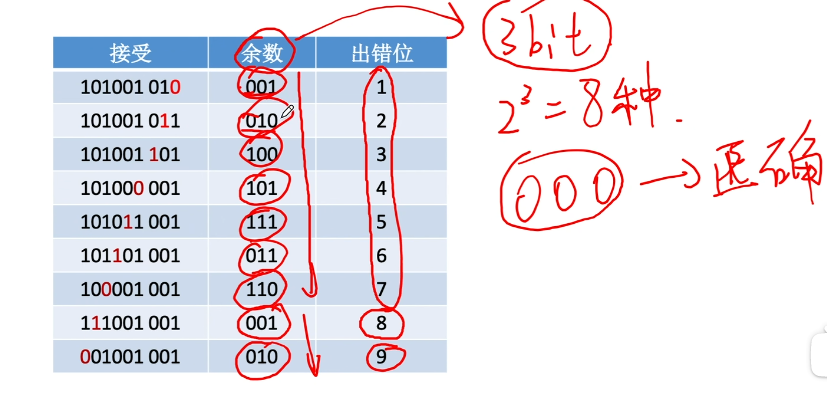
也具有纠错能力
K个信息位,R个校验位,若生成多项式选择得当,旦
,则CRC码可纠正1位错
在信息位不多的情况下,CRC码可以进行纠错
比如:
信息位:0100
生成多项式:
0100 000 对1101模2除,余数为011
CRC码:0100 011
理论上可以证明循环冗余校验码的检错能力有以下特点:
- 1)可检测出所有奇数个错误;
- 2)可检测出所有双比特的错误;
- 3)可检测出所有小于等于校验位长度的连续错误;
总结:
2.2 定点数的表示与运算
2.2.1定点数的表示
通常只有无符号整数,而没有无符号小数
- 定点数:小数点位置固定
- Eg:996.007 — 常规计数
- 浮点数:小数点的位置不固定
- Eg:
— 科学计数法
- Eg:
二进制的定点数、浮点数也类似
无符号数的表示
整个机器字长的全部二进制位均为数值位,没有符号位,相当于数的绝对值。
【例】1001 1100B
$=12^7+02^6+02^5+12^4+12^3+12^2+02^1+02^0$

表示范围:
8位二进制数:
0000 0000 ~ 1111 1111 = 1 0000 0000 -1
0 ~ 255 =
n位无符号为的表示范围为:0 ~
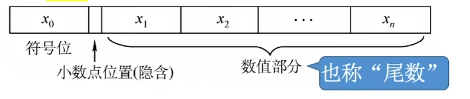
有符号数的定点表示
定点整数:

常写为:
若为指明机器字长,也可写为:
定点小数:
常写为:
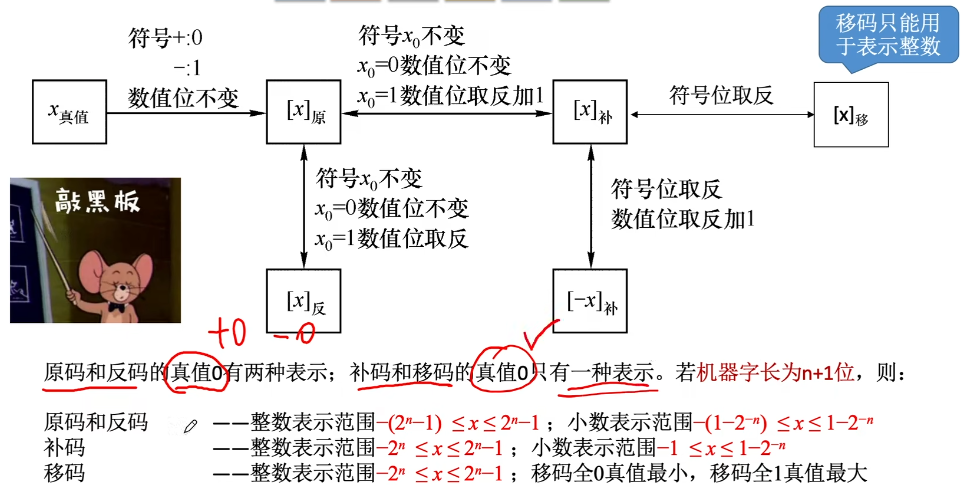
注:可用原码、反码、补码三种方式来表示定点整数和定点小数。还可以用移码表示定点整数。
若真值为x,则用
原码
用尾数表示真值的绝对值,符号位“0/1”对应“正/负”
若机器字长为n+1位,则尾数占n位。
原码整数的表示范围
- 关于原点对称
- 真值0有+0 和 -0两种形式
原码小数的表示范围:
- 关于原点对称
- 真值0有+0 和 -0两种形式
反码
若符号位为0, 则反码与原码相同
若符号位为1,则数值位全部取反
定点整数的表示:
X = +19D
X = -19D
若机器字长n+1位,反码整数的表示范围
- 真值0有+0 和 -0两种形式

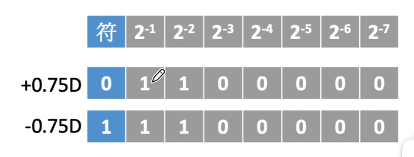
定点小数的表示:
X = +0.75D
X = - 0.75D
- 若机器字长n+1位, 反码小数的表示范围
- 真值0有+0 和 -0两种形式
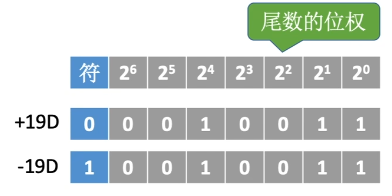
补码
正数的补码 = 原码
负数的补码 = 反码+1(要考虑进位)
将负数补码转回原码的方法相同:尾数取反,末位+1
定点整数的表示:
X = +19D
X = -19D
- 若机器字长n+1位,补码整数的表示范围
- 比原码多表示一个
定点小数的表示:
X = +0.75D
X = - 0.75D
- 若机器字长n+1位,补码小数的表示范围
- 比原码多表示一个-1
注意!补码的真值0只有一种表示形式
移码
补码的基础上将符号位取反。
注意:移码只能用于表示正数。
定点整数的表示:
X = +19D
X = -19D
- 若机器字长n+1位,补码整数的表示范围
- 比原码多表示一个
注意!移码的真值0只有一种表示形式
不同码之间的转换

技巧:由
符号位、数值位全部取反,末位+1
总结
2.2.2原码补码移码的作用
模运算的定义

(mod 12)把所有整数分为12类(余数为0~11)
mod 12 余数相同的数,都是同一类,都是等价的
 模 - a的绝对值 = a 的补数
模 - a的绝对值 = a 的补数
加减运算
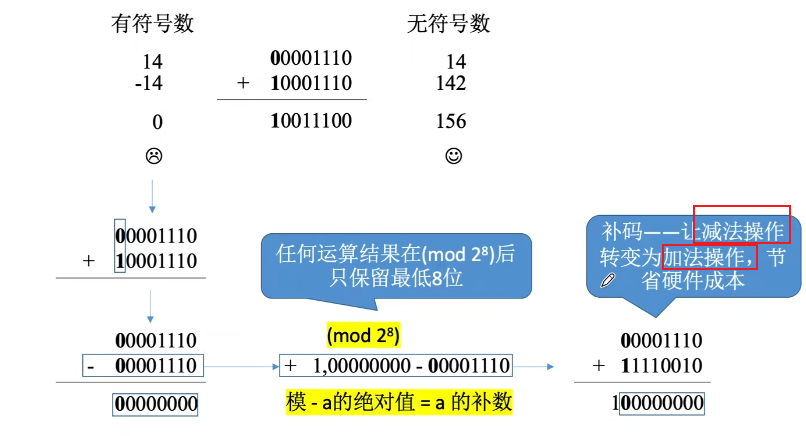
补码的作用:
使用补码可将减法操作转变为等价的加法,ALU中无需集成减法器。执行加法操作时,符号位一起参与运算
移码的作用:
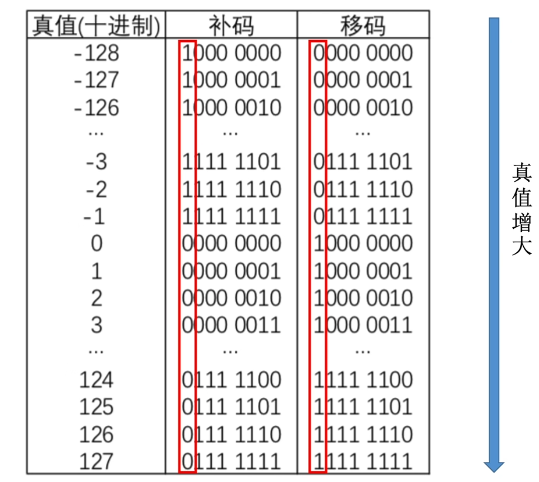
移码表示的整数很方便的对比大小
2.2.3移位运算
移位:通过改变各个数码位和小数点的相对位置,从而改变各数码位的位权。可用移位运算实现乘法、除法
算数移位

原码的算数移位:
原码的算数移位:符号位保持不变,仅对数值位进行移位
右移:
高位补0,低位舍弃。若舍弃的位=0,则相当于 除 2;若舍弃的位!= 0,则会丢失精度
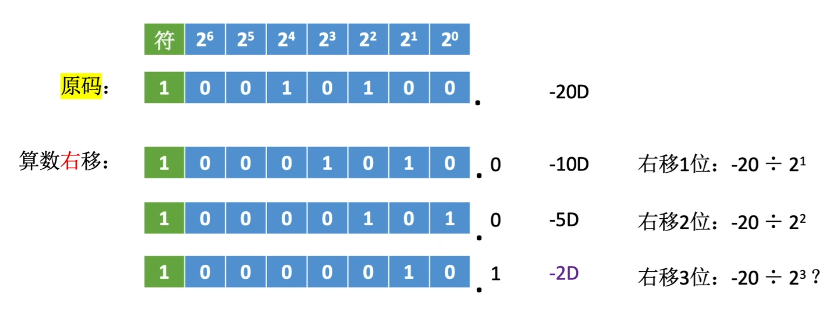
左移:
低位补0,高位舍弃。若舍弃的位=0,则相当于×2;若舍弃的位!=0,则会出现严重误差

定点小数同理
反码的算数移位:
正数: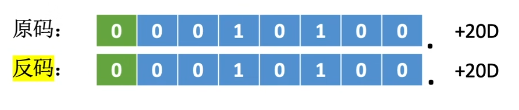
反码的算数移位―—正数的反码与原码相同,
因此对正数反码的移位运算也和原码相同。
右移:高位补0,低位舍弃。
左移:低位补0,高位舍弃。
负数: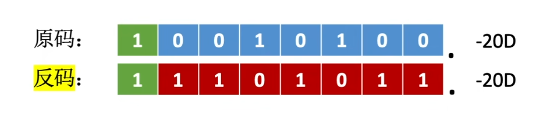
反码的算数移位――负数的反码数值位与原码相反,
因此负数反码的移位运算规则如下,
右移:高位补1,低位舍弃。
左移:低位补1,高位舍弃。
补码的算数移位:
正数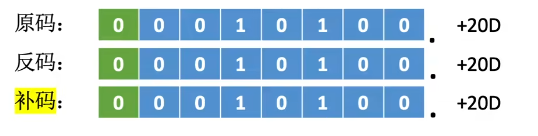
补码的算数移位一一正数的补码与原码相同,
因此对正数补码的移位运算也和原码相同。
右移:高位补o,低位舍弃。
左移::低位补o,高位舍弃。
负数:
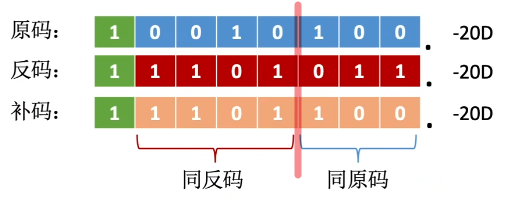
补码的算数移位――负数补码=反码末位+1
导致反码最右边几个连续的1都因进位而变为o,直到进位碰到第一个0为止。
规律―—负数补码中,最右边的1及其右边同原码。最右边的1的左边同反码负数补码的算数移位规则如下:
- 右移(同反码):高位补1,低位舍弃。
- 左移(同原码):低位补0,高位舍弃。
算数移位
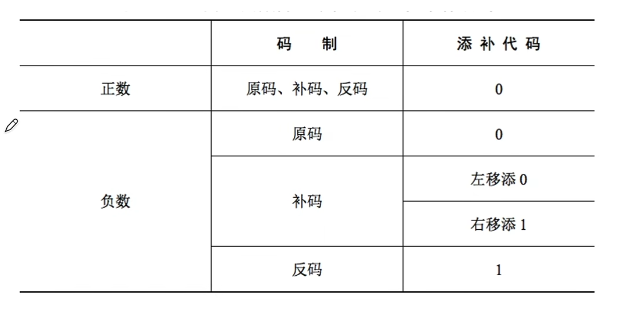
左移相当于 * 2;右移相当于 / 2
由于位数有限,因此有时候无法用算数移位精确地等效乘除法。
逻辑移位
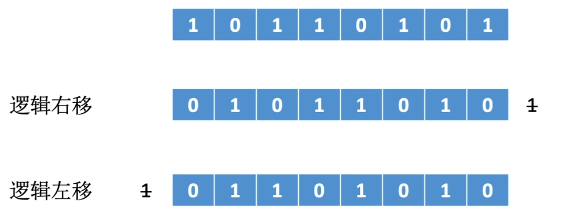
逻辑右移:高位补0,低位舍弃
逻辑左移:低位补0,高位舍弃
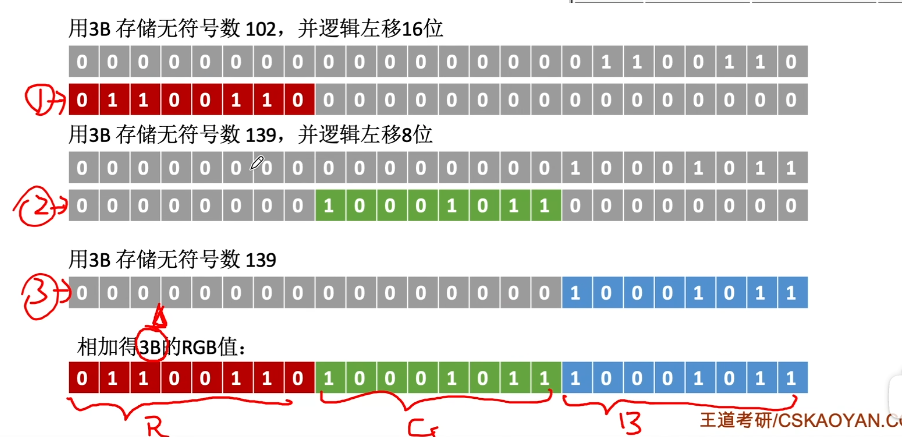
可以把逻辑移位看做是对”无符号位“的算数移位【移位举例】:
存储RGB:R = 102 01100110
G = 139 10001011
B = 139 10001011
循环移位
不带进位位的循环左移:
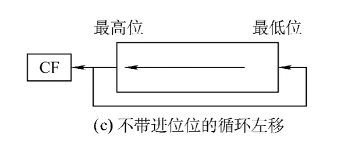


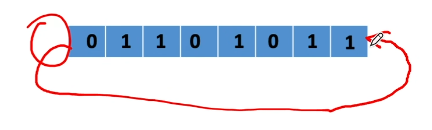
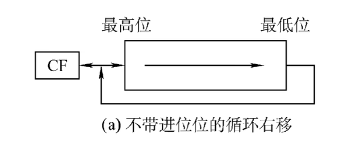
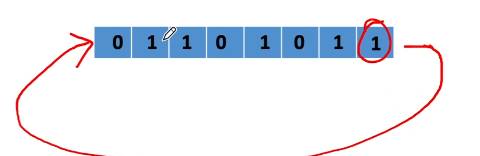
不带进位位循环右移:
带进位位的循环左移:
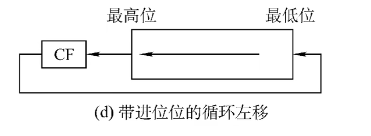
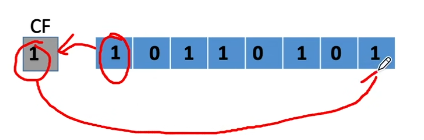
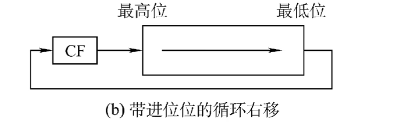
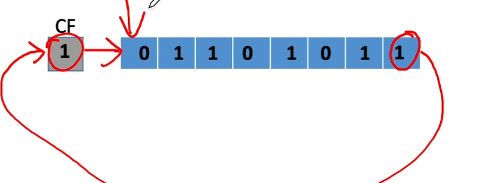
带进位位的循环右移:
总结
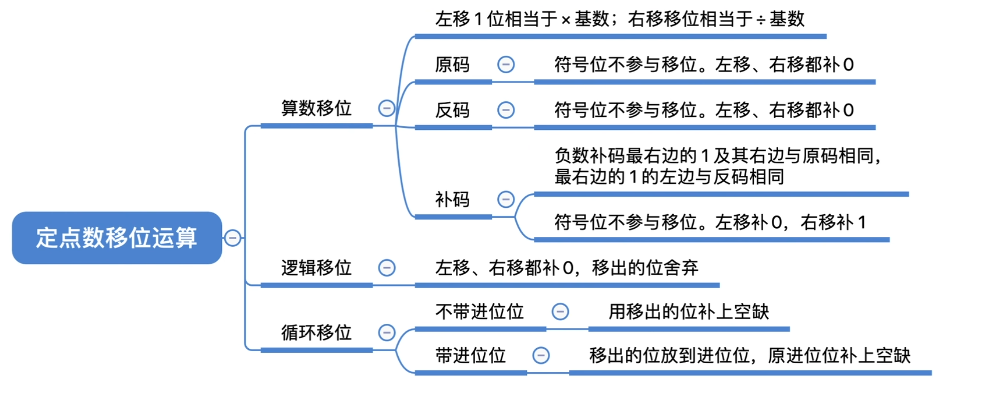
注意:由于原、反、补码位数有限,因此某些时候算数移位不能精确等效乘法、除法
2.2.4加减运算和溢出判断
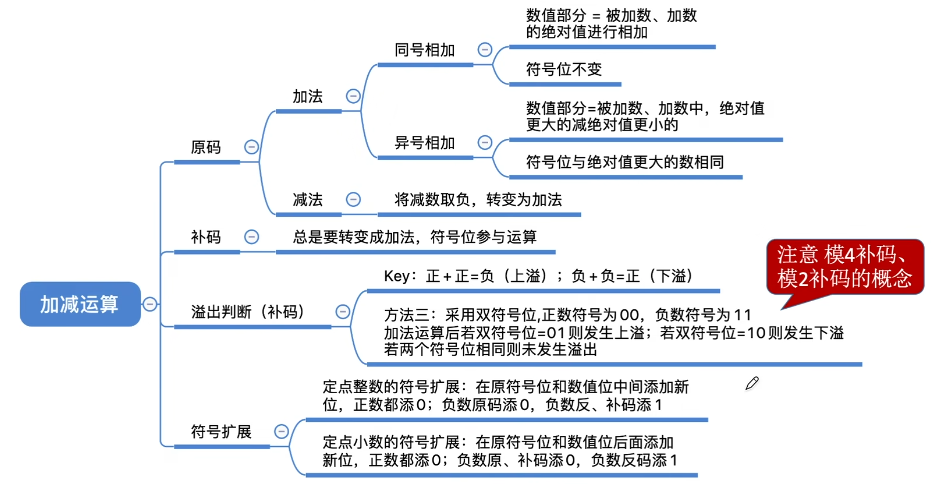
原码的加减运算
直接对原码进行加法运算,可能出错

用减法器实现:
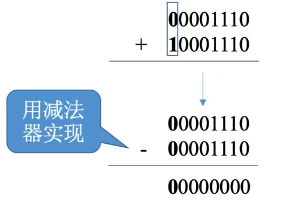 原码的加法运算:
原码的加法运算:
- 正+正→绝对值做加法,结果为正
- 负+负→绝对值做加法,结果为负
- 正+负→绝对值大的减绝对值小的,符号同绝对值大的数
- 负+正→绝对值大的减绝对值小的,符号同绝对值大的数
正 + 正,负 + 负 结果可能会溢出
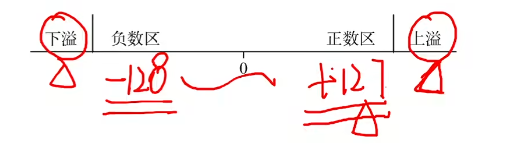
原码的减法运算:“减数”符号取反,转变为加法: - 正-负→正+正 - 负-正→负+负 - 正-正→正+负 - 负+正→负-负 #### 补码的加减运算 设机器字长为8位(含1位符号位),A = 15,B= -24,求
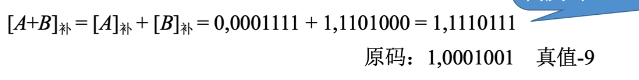
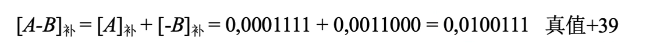
 逻辑表达式:
- 与:如ABC,表示A与B与C
- 仅当A、B、C均为1时,ABC为1
- A、B、C有一个或多个为0时,ABC为0
- 或:如A+B+C,表示A或B或C
- 仅当A、B、C均为0时,A+B+C为0
- A、B、C中有一个或多个为1,则A+B+C.
- 非:如
逻辑表达式:
- 与:如ABC,表示A与B与C
- 仅当A、B、C均为1时,ABC为1
- A、B、C有一个或多个为0时,ABC为0
- 或:如A+B+C,表示A或B或C
- 仅当A、B、C均为0时,A+B+C为0
- A、B、C中有一个或多个为1,则A+B+C.
- 非:如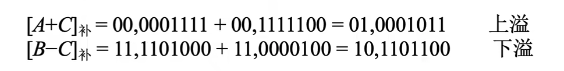 记两个符号位为
记两个符号位为符号拓展
int —> long ,短数据—> 长数据。
整数:
正整数:

负整数:
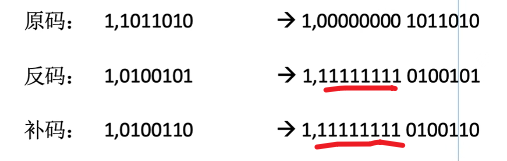 定点整数的符号扩展:
- 在原符号位和数值位中间添加新位,正数都添0;
- 负数原码添0,负数反、补码添1
###### 小数:
正小数:
定点整数的符号扩展:
- 在原符号位和数值位中间添加新位,正数都添0;
- 负数原码添0,负数反、补码添1
###### 小数:
正小数:
 负小数:
负小数:
 定点小数的符号扩展:
- 在原符号位和数值位后面添加新位,正数都添0;
- 负数原、补码添0,负数反码添1
##### 总结
定点小数的符号扩展:
- 在原符号位和数值位后面添加新位,正数都添0;
- 负数原、补码添0,负数反码添1
##### 总结
 ### 2.2.5定点数的乘法运算
### 2.2.5定点数的乘法运算
 手算乘法(十进制)
手算乘法(十进制)
 手算乘法(二进制)
手算乘法(二进制)
 #### 原码的乘法运算
实现方法:先加法再移位,重复n次
符号单独处理:符号位 =
#### 原码的乘法运算
实现方法:先加法再移位,重复n次
符号单独处理:符号位 = 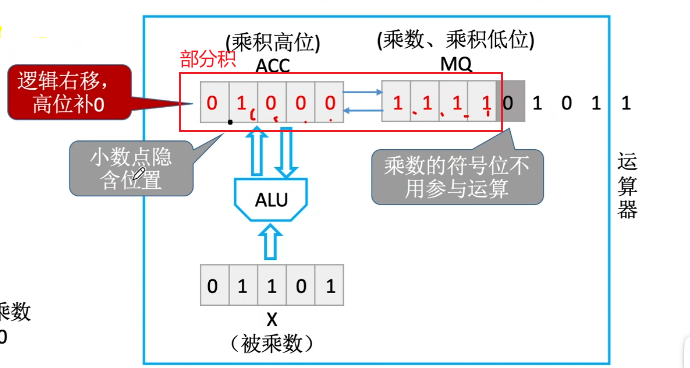 求解过程:
求解过程:
 原码一位乘法:(机器字长n+1,数值部分占n位)
- 符号位通过异或确定;
- 数值部分通过被乘数和乘数绝对值的n轮加法、移位完成
- 根据当前乘数中参与运算的位确定(ACC)加什么。
- 若当前运算位=1,则(ACC)+
原码一位乘法:(机器字长n+1,数值部分占n位)
- 符号位通过异或确定;
- 数值部分通过被乘数和乘数绝对值的n轮加法、移位完成
- 根据当前乘数中参与运算的位确定(ACC)加什么。
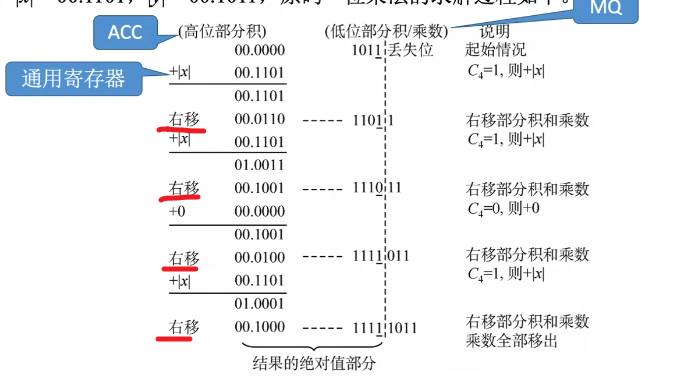
- 若当前运算位=1,则(ACC)+补码的乘法运算
进行n轮加法、移位,最后再多来一次加法
每次加法可能+0、+
- 根据当前MQ中的最低位、辅助位来确定加什么
- 辅助位 - MQ中最低位=1时,(ACC)+
- 辅助位 - MQ中最低位=0时,(ACC)+0
- 辅助位 - MQ中最低位=-1时,(ACC)+
- 辅助位 - MQ中最低位=1时,(ACC)+
每次移位都是“补码的算数右移”
符号位参与运算运算器中:
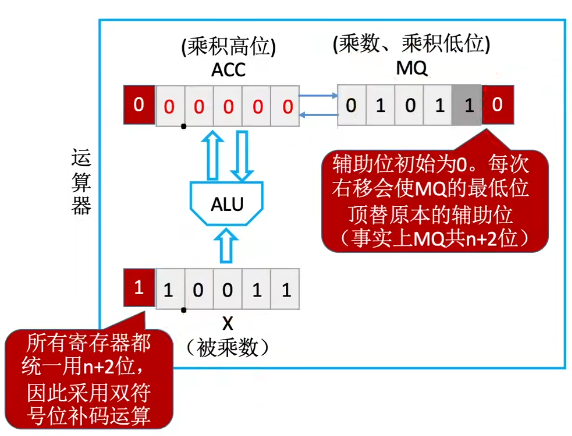
手算模拟:
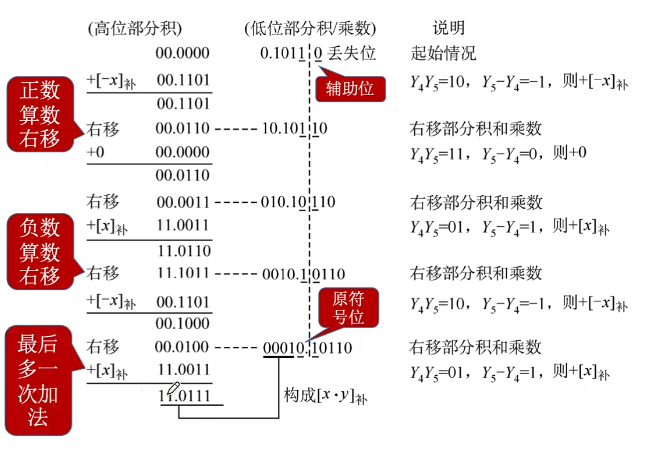
补码的算数右移:
符号位不动,数值位右移,正数右移补0,负数右移补1(符号位是啥就补啥)
2.2.6定点数的除法运算
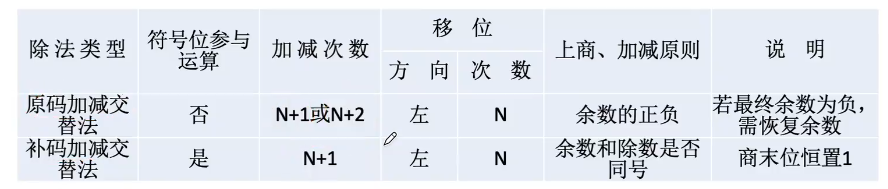
原码的除法运算
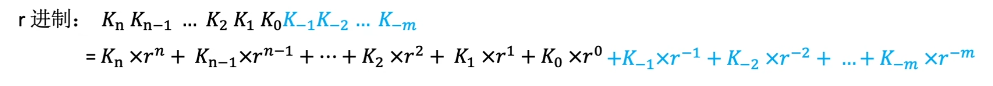
手算除法(十进制)
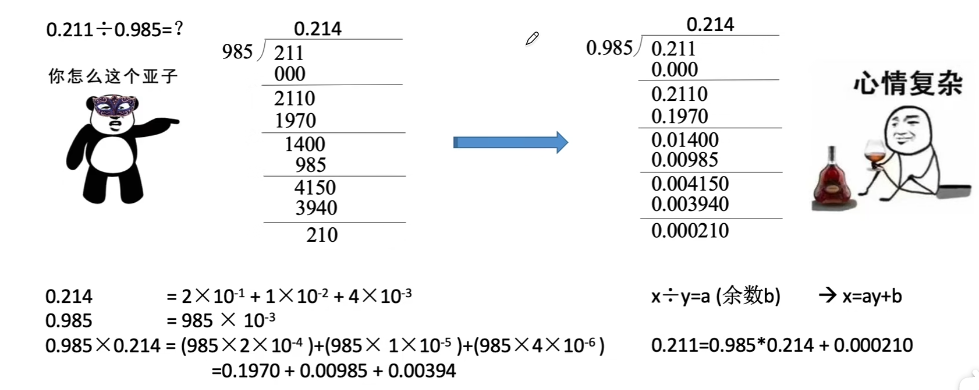
手算除法(二进制)

x/y的结果为0.1101,余数为0.00000111
规律:忽略小数点,每确定一位商,进行一次减法,得到4位余数,在余数末尾补0,再确定下一位商。确定5位商即可停止(机器字长为5位)
恢复余数法
符号单独处理:符号位 =
数值位取绝对值进行除法计算
实现方法:上商0/1,得到余数,余数末尾补0
运算器中:
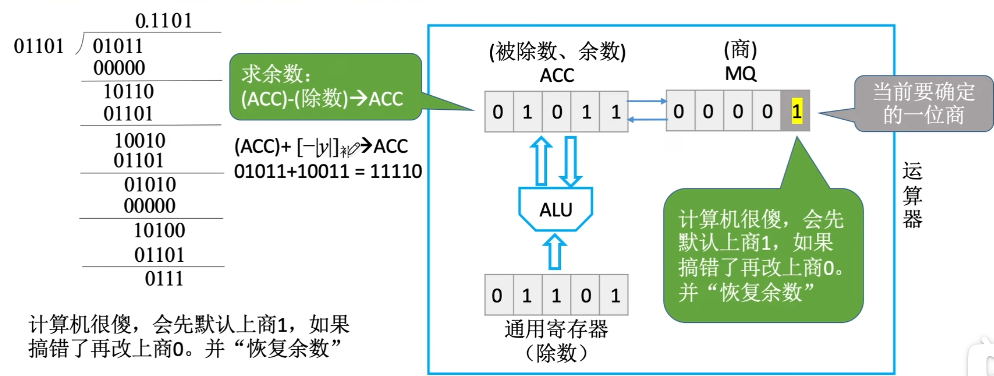
当计算完之后:之前商1是错的。
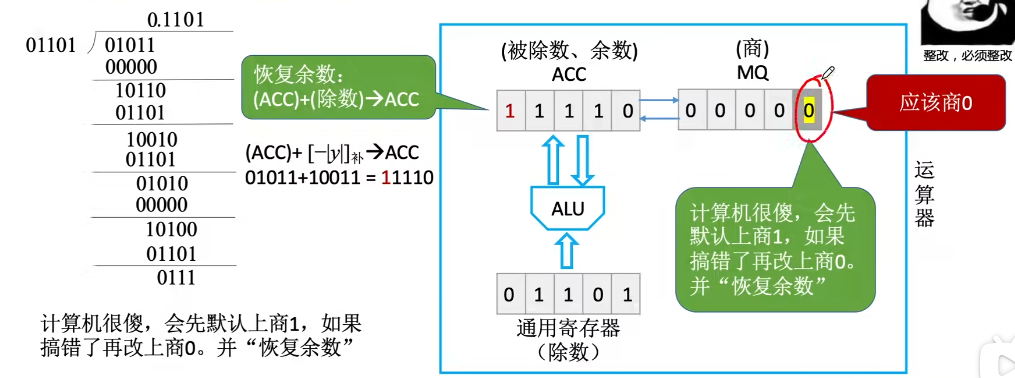
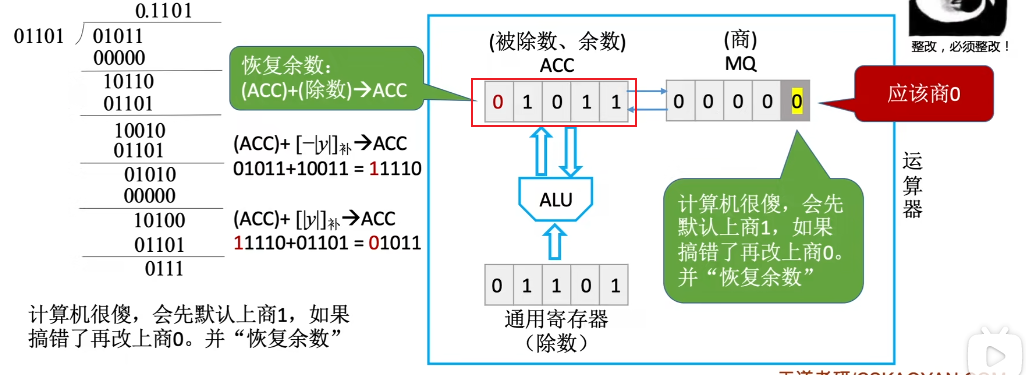
所以要恢复余数:
(ACC) + (除数) —> ACC
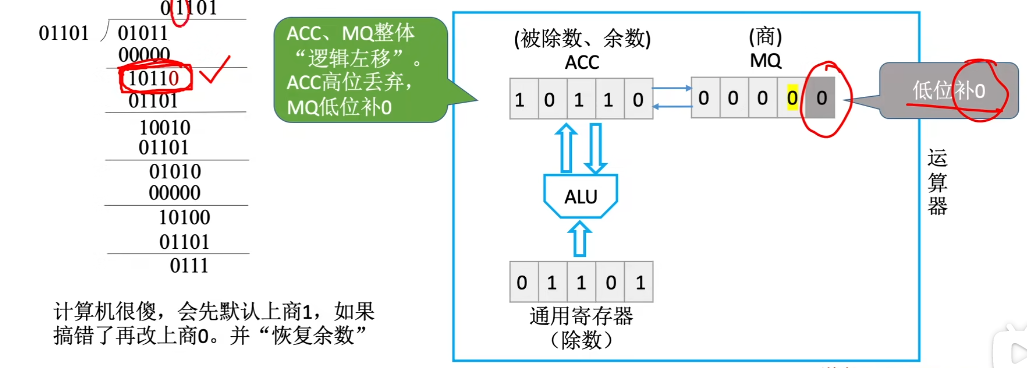
逻辑左移:
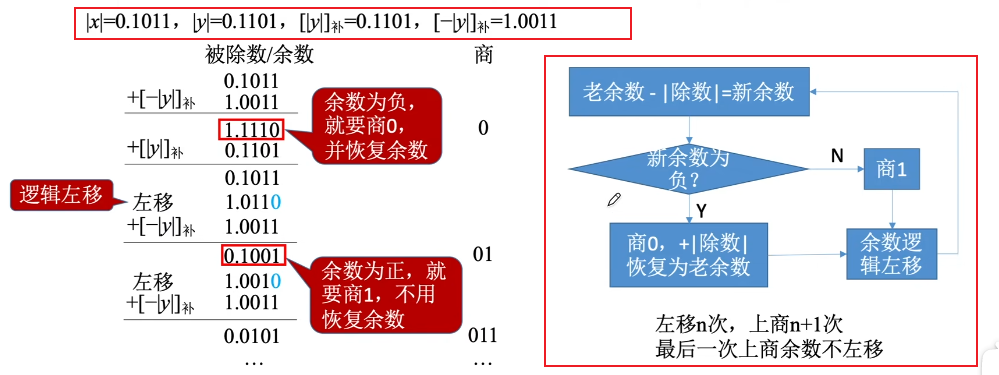
手算:
设机器字长为5位(含1位符号位,n=4),x = 0.1011,y = 0.1101采用原码恢复余数法求x/y
加减交替法(不恢复余数法)
 注:余数的正负性与商相同
注:余数的正负性与商相同
恢复余数法:当余数为负时商0,并+|除数|,再左移,再-|除数|
加减交替法:当余数为负时商0,并左移,再+|除数|
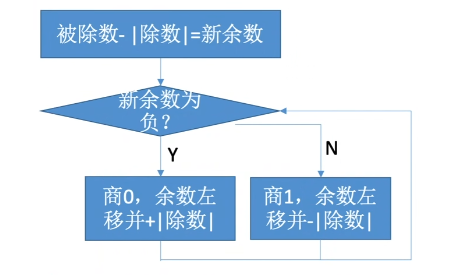
加/减n+1次,每次加减确定一位商;
左移n次(最后一次加减完不移位)最终可能还要再多一次加
补码的除法运算
符号位参与运算
被除数/余数、除数采用双符号位
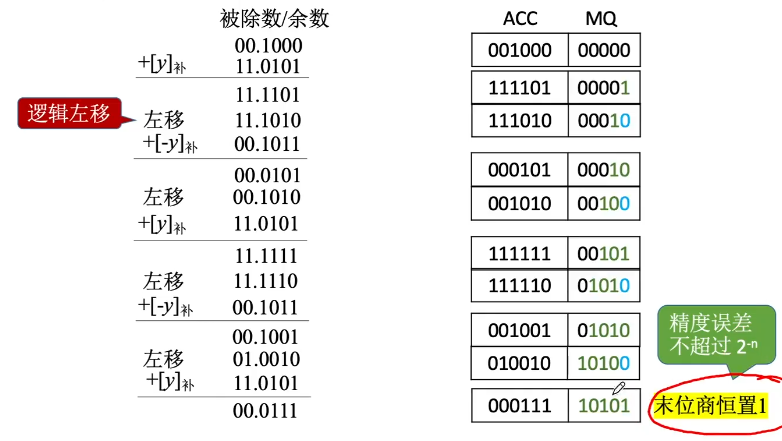
被除数和除数同号,则被除数减去除数;
异号则被除数加上除数。
余数和除数同号,商1,余数左移一位减去除数;
余数和除数异号,商0,余数左移一位加上除数。
重复N次。
回顾
2.2.7数据的存储和排列
大小端模式

边界对齐
现代计算机通常是按字节编址,即每个字节对应1个地址
通常也支持按字、按半字、按字节寻址。
假设存储字长为32位,则1个字=32bit,半字=16bit。每次访存只能读/写1个字
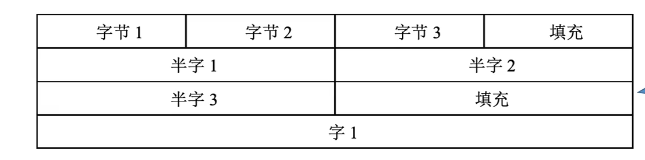
访问一个字/半字都只需要一次访存
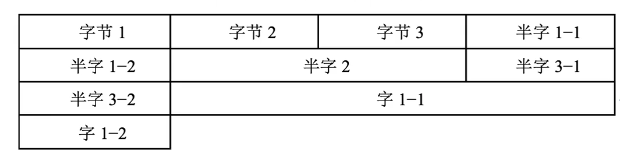
访问一个字/半字可能需要两次访存
相比较来说,边界对齐是一种空间换时间的策略。
2.3 浮点数的表示与运算
定点数的局限性:定点数可表示的数字范围有限,但我们不能无限制地增加数据的长度。
2.3.1浮点数的表示
定点数:如纯小数0.1011和纯整数11110
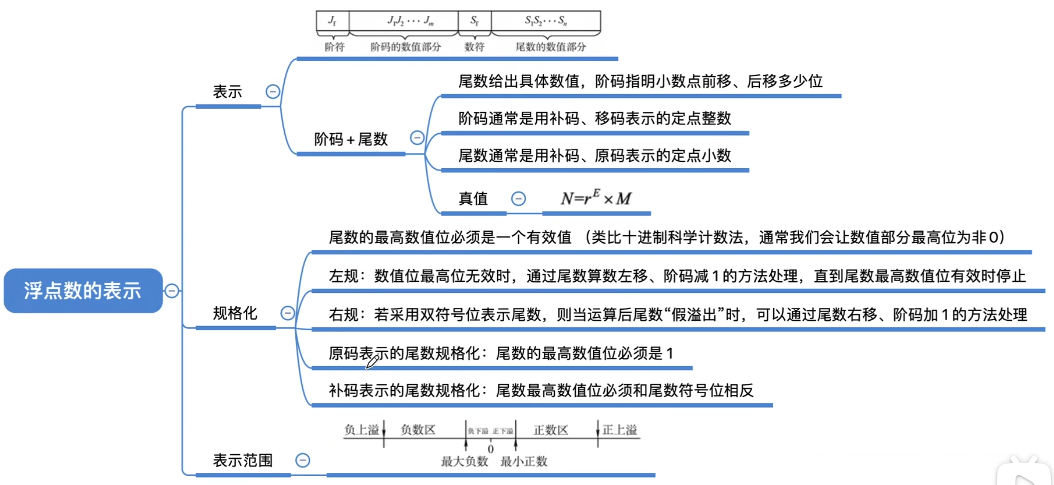
浮点数:
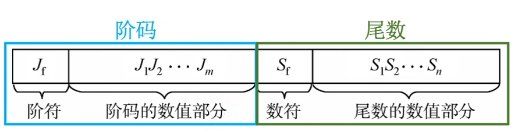
阶码:常用补码或移码表示的定点整数
- 阶码E反映浮点数的表示范围及小数点的实际位置;
尾数:常用原码或补码表示的定点小数
- 尾数M的数值部分的位数n反映浮点数的精度。
尾数给出一个小数,阶码指明了小数点要向前/向后移动几位
浮点数的真值:
浮点数的规格化
规格化浮点数:规定尾数的最高数值必须是一个有效值
b = 0,10; 0.01001

尾数算数左移1位,阶码减1。直到尾数最高位是有效值(左规)
左规
- 当浮点数运算的结果为非规格化时要进行规格化处理,将尾数算数左移一位,阶码减1。
右规
- 当浮点数运算的结果尾数出现溢出(双符号位为01或10)时,将尾数算数右移一位,阶码加1。
【例】

注:采用“双符号位”,当移除发生时,可以挽救。更高的符号位是正确的符号位。
规格化浮点数的特点
1.用原码表示的尾数进行规格化:
规格化的原码尾数,最高数值位一定是1
- 正数
- 正数为0.1* 的形式,其最大值表示为0.11…..1;最小值表示为0.10…0
- 尾数的表示的范围为
。
- 负数
- 负数为1.1* 的形式,其最大值表示为1.10…0;最小值表示为1.11…1
- 尾数的表示的范围为
。
2.用补码表示的尾数进行规格化:
规格化的补码尾数,符号位与最高数值位一定相反
- 正数
- 正数为0.1* 的形式,其最大值表示为0.11…..1;最小值表示为0.10…0
- 尾数的表示的范围为
。
- 负数
- 负数为1.0* 的形式,其最大值表示为1.01…1;最小值表示为1.00…0
- 尾数的表示的范围为
。
注:补码算数左移,低位补0;补码算数右移,高位补1.
总结
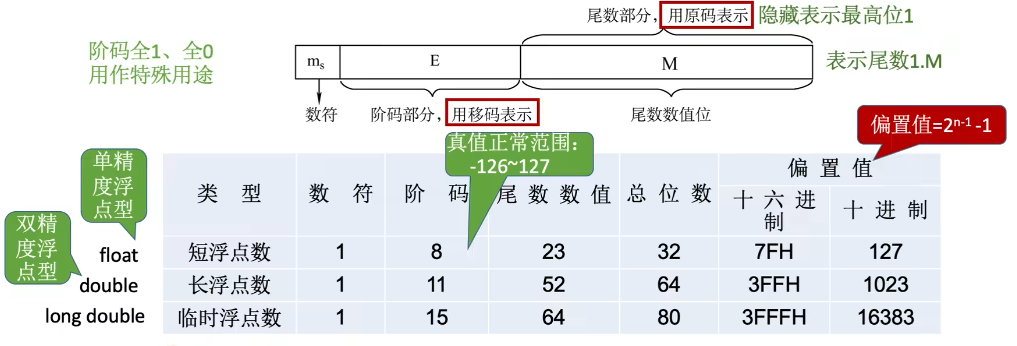
2.3.2 浮点数的标准(IEEE 754)
移码:补码的基础上将符号位取反。【注意:移码只能用于表示整数】
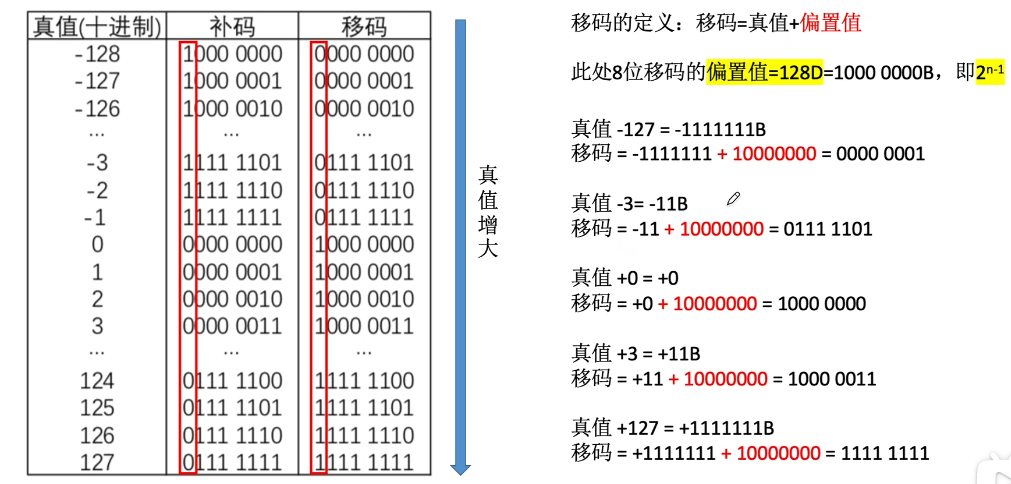
移码的定义:移码 = 真值 + 偏置值
偏置值一般取
阶码真值 = 移码 - 偏移量
规格化的短浮点数的真值为:$(-1)^s 1.M 2^{E-127}$
规格化的长浮点数的真值为:$(-1)^s 1.M 2^{E-1023}$
【例】将十进制数-0.75转换为IEEE 754的单精度浮点数格式表示:

【例】IEEE 754的单精度浮点数 C0 A0 00 00 H的值是多少

IEEE 754单精度浮点型能表示的最小绝对值、最大绝对值是多少?
最小绝对值:尾数全为0,阶码真值最小-126,对应移码机器数0000 0001此时整体的真值为
最大绝对值:尾数全为1,阶码真值最大127,对应移码机器数1111 1110此时整体的真值为

阶码全1、全0用作特殊用途
只有1 <= E < 254,真值 =- 当阶码E全为0,尾数M不全为0时,表示非规格化小数
- 当阶码E全为0,尾数M全为0时,表示真值
0 - 当阶码E全为1,尾数M全为0时,表示无穷大
- 当阶码E全为1,尾数M不全为0时,表示非数值“NaN”(Not a Number)
- 如 0 / 0,
等非法运算的结果就是NaN
- 如 0 / 0,
由浮点数确定真值(阶码不是全0、也不是全1):
1.根据“某浮点数”确定数符、阶码、尾数的分布
2.确定尾数1.M(注意补充最高的隐含位1)
3.确定阶码的真值=移码-偏置值﹑(可将移码看作无符号数,用无符号数的值减去偏置值)
4.
2.3.3浮点数的运算
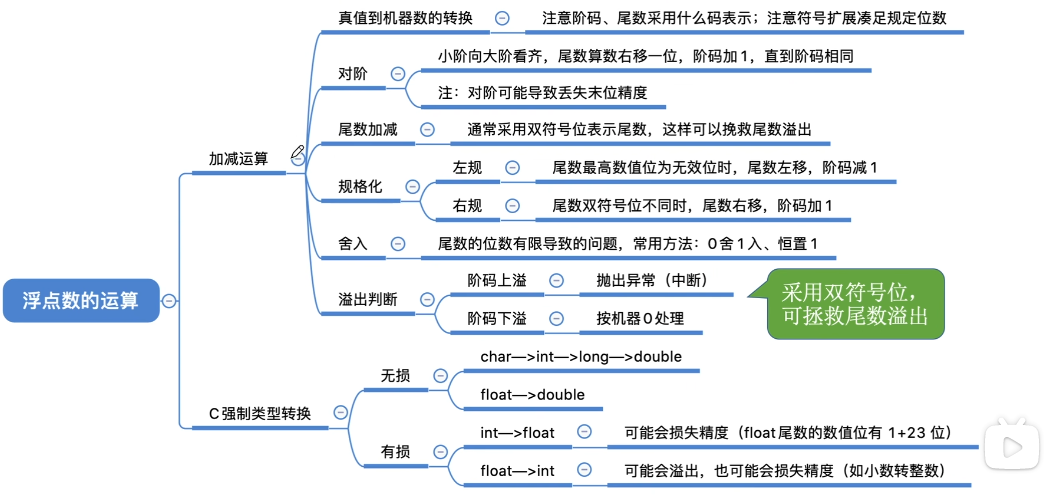
十进制的

为什么小阶向大阶靠起?
方便计算机对尾数处理。
浮点数的加减运算
【例】已知十进制数X=-5/256、Y=+59/1024,按机器补码浮点运算规则计算X-Y,结果用二进制表示,浮点数格式如下∶阶符取2位,阶码取3位,数符取2位,尾数取9位

舍入
如:加减结果为11100,10.110001011
“0”舍“1”入法:类似于十进制数运算中的“四舍五入”法,即在尾数右移时,被移去的最高数值位为0,则舍去:被移去的最高数值位为1,
则在尾数的末位加1。这样做可能会使尾数又溢出,此时需再做一次右规。
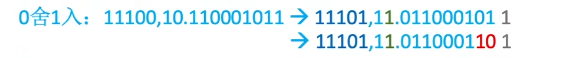
恒置“1”法:尾数右移时,不论丢掉的最高数值位是“1”还是“0”,都使右移后的尾数末位恒置“1”。这种方法同样有使尾数变大和变小的两种
可能。
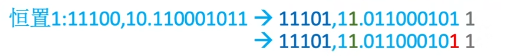
判断溢出:
强制类型转换
char —> int —> long —> double
float—> double
范围、精度从小到大,转换过程没有损失
32位:
- int:表示整数,范围
~ - float:表示整数及小数,范围
- int—> float :可能损失精度
- float—>int:可能溢出及损失精度
总结:
2.4 算术逻辑单元(ALU)
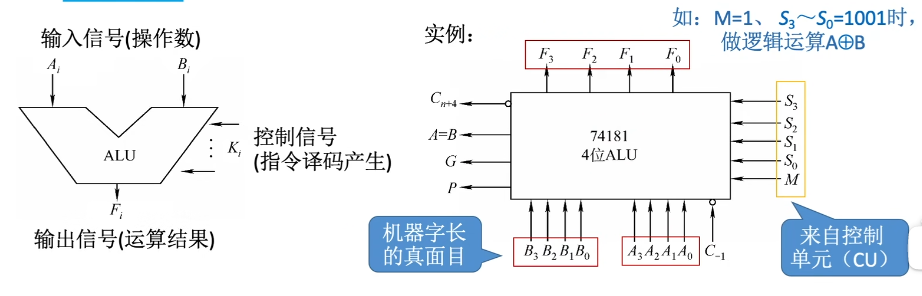
2.4.1加法器
一位全加器
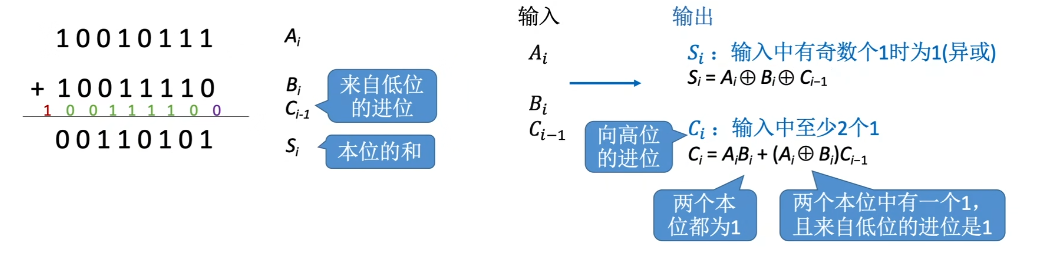
电路设计
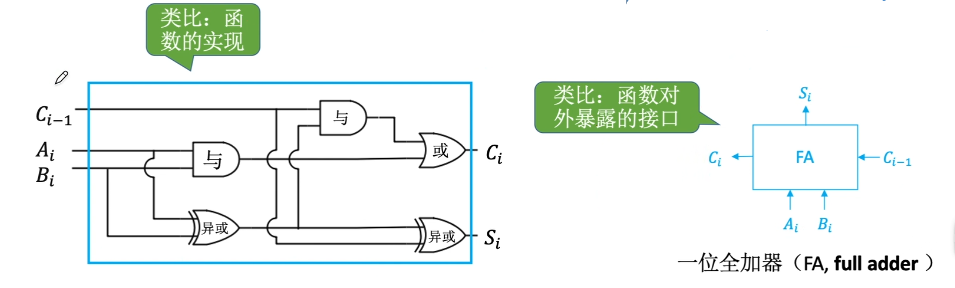
串行加法器
只有一个全加器,数据逐位串行送入加法器中进行运算。进位触发器用来寄存进位信号,以便参与下一次运算。
如果操作数长n位,加法就要分n次进行,每次产生一位和,并且串行逐位地送回寄存器。
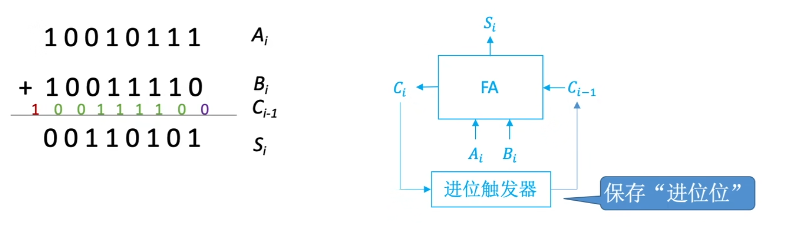
串行进位的并行加法器
串行进位的并行加法器:把n个全加器串接起来,就可以进行两个n位数的相加
串行进位又称为行波进位,每一级进位直接依赖于前一级的进位,即进位信号是逐级形成的。
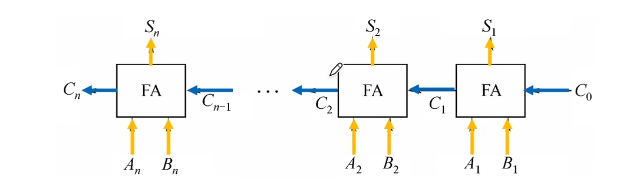
总结:
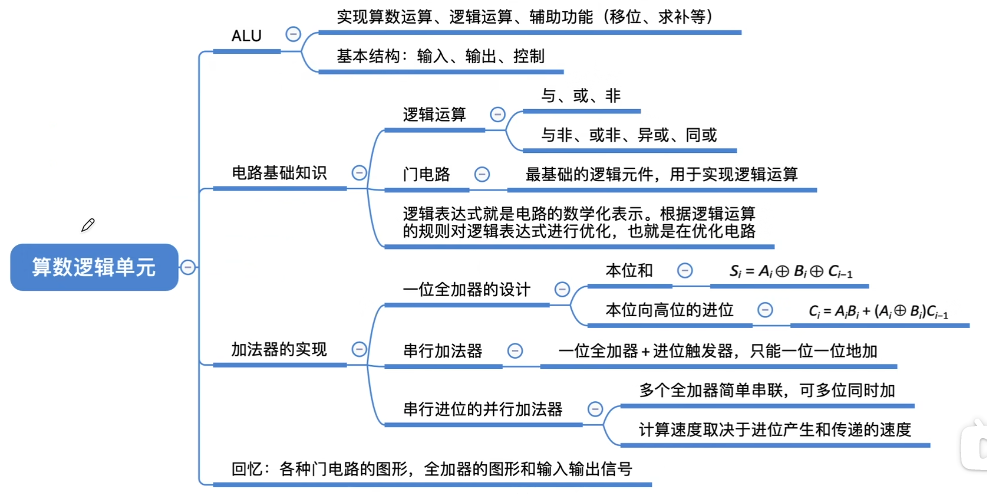
2.4.2加法器、ALU的改进
如何更快的产生进位
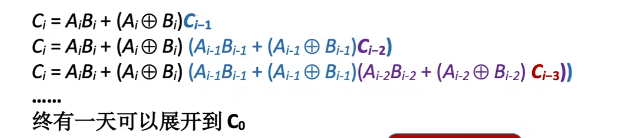
结论:第i位向更高维的进位
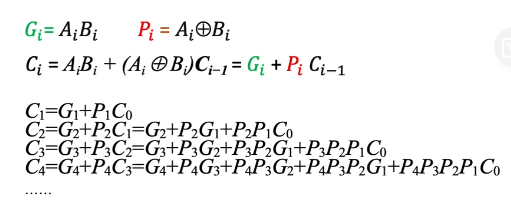
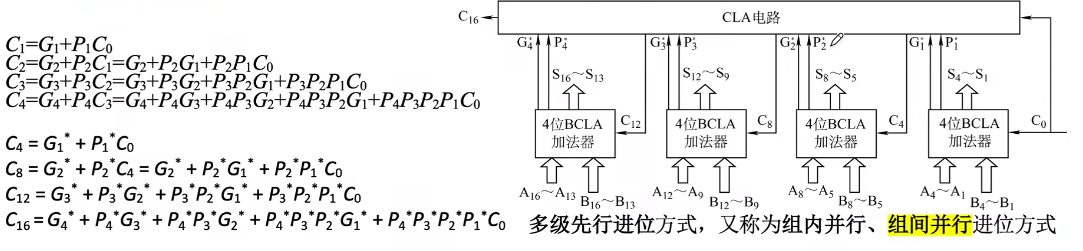
并行进位的并行加法器:各级进位信息同时形成,又称为先行进位、同时进位
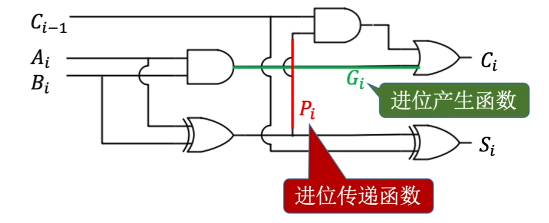
由4个FA和一些新的线路、运算逻辑组成
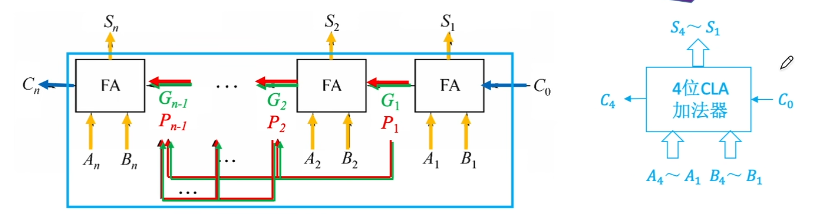
单级先行进位方式,又称组内并行、组间串行进位方式。
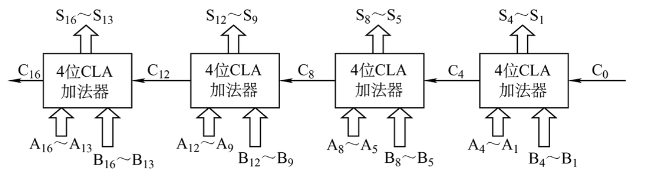
组内进位信号:
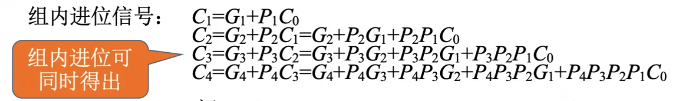
记:
核心特性:根据本组的 4
组内进位信号:
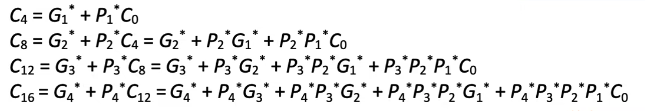
多级先行进位方式,又称组内并行、组间并行进位方式。